山东省聊城市高唐县2022年中考一模数学试题

更新时间：2022-05-16 浏览次数：87 类型：中考模拟

一、单选题

1. (2023七下·磁县月考) 与 $\text{[math]}$ 最接近的整数是（）

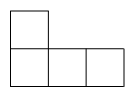
A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
2. (2022·高唐模拟) 如图，该立体图形的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·高唐模拟) 如图，已知 $\text{[math]}$ ，将一个含45°角的三角尺按图中方式放置， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 21° B . 24° C . 30° D . 66°

答案解析收藏纠错 + 选题
4. (2024八下·从江期末) 下列等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·高唐模拟) 下列四个命题中，真命题有（）
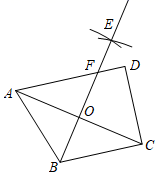
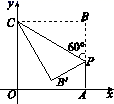
①两条直线被第三条直线所截，同位角相等；②实数与数轴上的点是一一对应的；③三角形的一个外角大于任何一个内角；④平面内点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距离是2．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
6. (2022·高唐模拟) 某校九年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形统计图与扇形统计图，依据图中信息，得出下列结论，表中错误的是（）

A . 接受这次调查的家长人数为200 B . 表示“无所谓”的家长人数为40 C . 在扇形统计图中，表示“不赞同”的家长部分所对应的扇形圆心角的大小为162° D . 随机抽查一名接受调查的家长，恰好抽到表示“很赞同”的家长的概率是 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·海淀模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则式子 $\text{[math]}$ 的值是（）

A . 48 B . $\text{[math]}$ C . 16 D . 12

答案解析收藏纠错 + 选题
8. (2022·高唐模拟) 在数轴上有不同的两点A、B，其中点A表示的数是 $\text{[math]}$ ，点B表示的数是 $\text{[math]}$ ，如果A，B两点关于原点对称，那么 $\text{[math]}$ 的值是（）

A . -2 B . 0 C . 2 D . 0或2

答案解析收藏纠错 + 选题
9. (2022·高唐模拟) 如图，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，分别以点A，C为圆心，大于 $\text{[math]}$ 长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（）

A . $\text{[math]}$ B . 6 C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
10. (2022·高唐模拟) 如图，在平面直角坐标系中，四边形OABC是正方形，点A的坐标是（4，0），P为边AB上一点，∠CPB=60°，沿CP折叠正方形OABC ，折叠后，点B落在平面内的点B'处，则点B'的坐标为（）

A . （2， $\text{[math]}$ ） B . （ $\text{[math]}$ ， $\text{[math]}$ ） C . （2， $\text{[math]}$ ） D . （ $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
11. (2022·高唐模拟) 如图，在正五边形 $\text{[math]}$ 中，连接 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画弧交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022·高唐模拟) 算筹是古代用来进行计算的工具，它是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图）．当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间：个位、百位、万位数用纵式表示；十位，千位，十万位数用横式表示；“0”用空位来代替，以此类推．例如3306用算筹表示就是，则2022用算筹可表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

13. (2023七上·咸阳期末) 已知关于x的方程3x﹣2k＝2的解是x＝k﹣2，则k的值是.

答案解析收藏纠错 + 选题
14. (2022八下·柳江期末) 某商场为了招聘商品拆装上架员工一名，设置了计算机、语言和商品知识三项测试，并对这三项测试成绩按照2：3：5的比确定.若某应试者三项测试成绩分别为70，50，80，则该应试者的平均成绩是.

答案解析收藏纠错 + 选题
15. (2022·海陵模拟) 用半径为30，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

答案解析收藏纠错 + 选题
16. (2022·高唐模拟) 如图，若菱形ABCD的顶点A，B的坐标分别为（3，0），（﹣2，0），点D在y轴上，则点C的坐标是．

答案解析收藏纠错 + 选题
17. (2022·高唐模拟) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别是AB，AC的中点，把△ABC绕着点C做逆时针旋转，得到 $\text{[math]}$ ，点D的对应点为 $\text{[math]}$ ，连接 $\text{[math]}$ ，则在旋转过程中 $\text{[math]}$ 的最大值与最小值的比值为．

答案解析收藏纠错 + 选题

三、解答题

18. (2022·高唐模拟) 不等式组 $\text{[math]}$
1. （1）解此不等式组；
2. （2）若m是此不等式组的最大整数解，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
19. (2022·高唐模拟) 为做好新冠疫情的防控工作，某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元，该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液．
1. （1）求甲、乙两种消毒液的零售价分别是每桶多少元？
2. （2）由于疫情防控进入常态化，该单位需再次购买两种消毒液共300桶，且甲种消毒液的桶数不少于乙种消毒液桶数的 $\text{[math]}$ ，由于购买量大，甲、乙两种消毒液分别获得了20元/桶，15元/桶的批发价．求甲种消毒液购买多少桶时，所需资金总额最少？最少总金额是多少元？
答案解析收藏纠错 + 选题
20. (2022·高唐模拟) 时代中学为了解学生对中国共产党党史知识的学习情况，在七年级和八年级举行了有关党史知识测试活动．现从七、八两个年级中各随机抽取20名学生的测试成绩（满分50分，30分及30分以上为合格；40分及40分以上为优秀）进行整理、描述和分析，给出了下面的部分信息．
七年级20名学生的测试成绩为：39，50，39，50，49，30，30，49，49，49，43，43，43，37，37，37，43，43，37，25．
八年级20名学生的测试成绩条形统计图如图所示；两个年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如表所示：
年级
平均数
众数
中位数
优秀率
七
41.1
a
43
m
八
39.5
44
b
n
请你根据上面提供的所有信息，解答下列问题：
1. （1）表中 $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ．根据样本统计数据，你认为该七、八年级中哪个年级学生掌握党史知识较好？并说明理由．（写一条理由即可）
2. （2）已知该中学七、八年级共1240名学生参加了此次测试活动，通过计算，估计参加此次测试活动成绩合格的学生人数能否超过1000．
3. （3）从样本中测试成绩为满分的七、八年级的学生中随机抽取两名学生，用列表或树状图法求两人在同一年级的概率．
答案解析收藏纠错 + 选题
21. (2022·高唐模拟) 如图，在矩形ABCD中，点E在边AD上，连接CE，以CE为边向右上方作正方形CEFG，作FH⊥AD，垂足为H，连接AF．
1. （1）求证：FH＝ED；
2. （2）若AB＝3，AD＝5，当AE＝1时，求∠FAD的度数．
答案解析收藏纠错 + 选题
22. (2022·高唐模拟) 如图所示的是一款机械手臂，由上臂、中臂和底座三部分组成，其中上臂和中臂可自由转动，底座与水平地面垂直．在实际运用中要求三部分始终处于同一平面内，其示意图如图1所示，经测量，上臂 $\text{[math]}$ ，中臂 $\text{[math]}$ ，底座 $\text{[math]}$
1. （1）若上臂AB与水平面平行， $\text{[math]}$ ．计算点A到地面的距离．
2. （2）在一次操作中，中臂与底座成 $\text{[math]}$ 夹角，上臂与中臂夹角为 $\text{[math]}$ ，如图2，计算这时点 $\text{[math]}$ 到地面的距离．与图1状态相比，这时点A向前伸长了多少?
答案解析收藏纠错 + 选题
23. (2022·高唐模拟) （已知在直角坐标系中，点A是反比例函数 $\text{[math]}$ 图象上的一个动点，连接AO并延长线交反比例函数 $\text{[math]}$ 的图象于点B，过点A作 $\text{[math]}$ 轴于点E．
1. （1）如图1，过点B作 $\text{[math]}$ 轴于点F，连接EF，BE，若 $\text{[math]}$ ，求△BOE的面积．
2. （2）如图2，过点E作 $\text{[math]}$ ，交反比例函数 $\text{[math]}$ 的图象于点P，连接OP．试探究：对于确定的实数k，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由．
答案解析收藏纠错 + 选题
24. (2022·高唐模拟) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为直径，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2022·高唐模拟) 如图1，在平面直角坐标系中，抛物线y＝－ $\text{[math]}$ $\text{[math]}$ ＋ $\text{[math]}$ x＋ $\text{[math]}$ 与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，对称轴与x轴交于点D．
1. （1）求直线BC的解析式；
2. （2）如图2，点P为直线BC上方抛物线上一点，连接PB、PC．当 $\text{[math]}$ 的面积最大时，在线段BC上找一点E(不与B、C重合)，使 $\text{[math]}$ $\text{[math]}$ BE的值最小，求点P的坐标和 $\text{[math]}$ $\text{[math]}$ BE的最小值；
3. （3）如图3，点G是线段CB的中点，将抛物线y＝－ $\text{[math]}$ $\text{[math]}$ ＋ $\text{[math]}$ x＋ $\text{[math]}$ 沿x轴正方向平移得到新抛物线 $\text{[math]}$ ， y′经过点D， $\text{[math]}$ 的顶点为F．在抛物线 $\text{[math]}$ 的对称轴上，是否存在一点Q，使得 $\text{[math]}$ 为直角三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题