B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 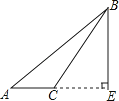


 B .
B .  C .
C .  D .
D . 





求证:点P在线段CD的垂直平分线上.

以下为证明过程,请在括号内填写出理论依据.
证明:
∵点P在线段AB的垂直平分线上,
∴PB=PA,( )
∵PC⊥PA,PD⊥PB,
∴∠DPB=∠CPA=90°.
在R△DPB和Rt△CPA中
,
∴Rt△DPB≌Rt△CPA( )
∴PD=PC( )
∴点P在线段CD的垂直平分线.( )



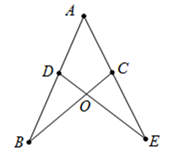
点B , C△ABC关于点P的等距点,线段PA , PB△ABC关于点P的等距线段;(填“是”或“不是”)