江苏省苏州市新区一中2021届九年级上学期数学期中联考试卷

更新时间：2024-07-13 浏览次数：194 类型：期中考试

一、单选题

1. (2020九上·苏州期中) 在Rt△ABC中，∠C=90°，AC=1，BC=3，则∠A的正切值为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·苏州期中) 方程x²=x的解是（）

A . x=1 B . x₁=﹣1，x₂=1 C . x₁=0，x₂=1 D . x=0

答案解析收藏纠错 + 选题
3. (2024九下·北京市模拟) 若正多边形的内角和是540°，则该正多边形的一个外角为（）

A . 45° B . 60° C . 72° D . 90°

答案解析收藏纠错 + 选题
4. (2020九上·苏州期中) 平面内有一点P到圆上最远的距离是 $\text{[math]}$ ，最近的距离是 $\text{[math]}$ ，则圆的半径是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 在半径为2的圆中，弦AB的长为2，则 $\text{[math]}$ 的长等于（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·苏州期中)
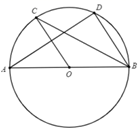
如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于( )

A . 8 B . 4 C . 10 D . 5

答案解析收藏纠错 + 选题
7. (2020九上·苏州期中) 如图，⊙O的直径AB=4，BC切⊙O于点B，OC平行于弦AD，OC=5，则AD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·苏州期中) 如图，矩形OCDE内接于扇形AOB，若点C是OA的中点，则∠BAD等于（）

A . 15° B . 18° C . 22.5° D . 30°

答案解析收藏纠错 + 选题
9. (2020九上·苏州期中) 如图，已知第一象限内的点A在反比例函数 $\text{[math]}$ 的图象上，第二象限的点B在反比例函数 $\text{[math]}$ 的图象上，且OA⊥OB，tanA=2，则k的值为（）

A . 4 B . 8 C . -4 D . -8

答案解析收藏纠错 + 选题
10. 如图， $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴的正半轴交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则点 $\text{[math]}$ 的纵坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·苏州期中) 已知a是关于x方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
12. (2024九上·沭阳期末) 一等腰三角形的两边长分别为4cm和6cm，则其底角的余弦值为．

答案解析收藏纠错 + 选题
13. (2020九上·苏州期中) 小明用一张扇形纸片做一个圆锥的侧面，已知该扇形的半径是10cm，弧长是12πcm² ，那么这个圆锥的高是cm.

答案解析收藏纠错 + 选题
14. (2020九上·苏州期中) 一元二次方程 $\text{[math]}$ 的两根为x₁ ， x₂ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
15. (2020九上·苏州期中) 如图，点A，B，D在⊙O上，∠A=20°，BC是⊙O的切线，B为切点，OD的延长线交BC于点C，则∠OCB=度.

答案解析收藏纠错 + 选题
16. (2020九上·苏州期中) 如图，⊙O是△ABC的外接圆，∠A＝45°，BC＝4，则⊙O的直径为.

答案解析收藏纠错 + 选题
17. (2020九上·苏州期中) 如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E为⊙G上一动点，CF⊥AE于F，当点E从B点出发顺时针运动到D点时，点F经过的路径长为.

答案解析收藏纠错 + 选题
18. (2020九上·苏州期中) 如图，在平面直角坐标系中，已知C（6，8），以点C为圆心的圆与y轴相切.点A、B在x轴上，且OA＝OB.点P为⊙C上的动点，∠APB＝90°，则AB长度的最大值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九上·武冈月考) 计算题
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2020九上·苏州期中) 解方程：
1. （1） 3（x﹣2）²＝x（x﹣2）；
2. （2） 3x²﹣6x+1＝0（用配方法）.
答案解析收藏纠错 + 选题
21. (2021九上·顺德期中) 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：
1. （1）每千克核桃应降价多少元？
2. （2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？
答案解析收藏纠错 + 选题
22. (2020九上·苏州期中) 如图，某数学活动小组为测量学校旗杆AB的高度，沿旗杆正前方 $\text{[math]}$ 米处的点C出发，沿斜面坡度 $\text{[math]}$ 的斜坡CD前进4米到达点D，在点D处安置测角仪，测得旗杆顶部A的仰角为37°，量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内，AB⊥BC，AB//DE.求旗杆AB的高度.（参考数据：sin37°≈ $\text{[math]}$ ，cos37°≈ $\text{[math]}$ ，tan37°≈ $\text{[math]}$ .计算结果保留根号）

答案解析收藏纠错 + 选题
23. (2021九下·苏州开学考) 如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E.
1. （1）求证：DE是⊙O的切线；
2. （2）若DE＝6，AE＝2 $\text{[math]}$ ，求⊙O的半径；
3. （3）在第（2）小题的条件下，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
24. (2020九上·乳山期末)
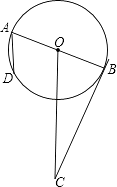
某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．

答案解析收藏纠错 + 选题
25. (2020九上·苏州期中) 如图，AB为⊙O的直径，C，D为圆上的两点，OC∥BD，弦AD，BC相交于点E.
1. （1）求证： $\text{[math]}$ ；
2. （2）若CE＝2，EB＝6，求⊙O的半径.
答案解析收藏纠错 + 选题
26. (2020九上·苏州期中) 在平面直角坐标系xOy中，已知点A(6，0)，点B(0，6)，动点C在以原点O为圆心，半径为3的⊙O上，连接OC，过点O作OD⊥OC，OD与⊙O相交于点D（其中点C，O，D按逆时针方向排列），连接AB.
1. （1）当OC//AB时，∠BOC的度数为.
2. （2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的最大值.
3. （3）连接AD，当OC//AD，点C位于第二象限时，
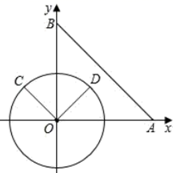
  ①求出点C的坐标；
  
  ②直线BC是否为⊙O的切线？并说明理由.
答案解析收藏纠错 + 选题
27. (2020九上·苏州期中) 已知在平面直角坐标系xOy中，直线l₁分别交x轴和y轴于点A(﹣3，0)，B(0，3).
1. （1）如图1，已知⊙P经过点O，且与直线l₁相切于点B，求⊙P的直径长；
2. （2）如图2，已知直线l₂：y=3x﹣3分别交x轴和y轴于点C和点D，点Q是直线l₂上的一个动点，以Q为圆心，2 $\text{[math]}$ 为半径画圆.
  ①当点Q与点C重合时，求证：直线l₁与⊙Q相切；
  
  ②设⊙Q与直线l₁相交于M，N两点，连结QM，QN.问：是否存在这样的点Q，使得△QMN是等腰直角三角形，若存在，求出点Q的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题