陕西省宝鸡市渭滨区新建路中学2021届九年级上学期数学期中考...

更新时间：2024-07-13 浏览次数：321 类型：期中考试

一、单选题

1. (2024九上·双流月考) 方程 $\text{[math]}$ 的根是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·兰陵期末) 在“众志成城，共战疫情”党员志愿者进社区服务活动中，小晴和小霞分别从“A，B，C三个社区”中随机选择一个参加活动，两人恰好选择同一社区的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·渭滨期中) 一元二次方程 $\text{[math]}$ 配方后可变形为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·渭滨期中) 点D是线段AB的黄金分割点（AD＞BD），若AB＝2，则BD＝（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ﹣1 D . 3﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·鼓楼月考) $\text{[math]}$ 是下列哪个一元二次方程的根（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·渭滨期中) 如图，下列条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，能使 $\text{[math]}$ 的条件的个数为（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
7. (2023九上·丹江口期末) 新冠病毒主要是经呼吸道飞沫传播的，在无防护下传播速度很快，已知有1个人患了新冠，经过两轮传染后共有625个人患了新冠，每轮传染中平均一个人传染m人，则m的值为（）.

A . 24 B . 25 C . 26 D . 27

答案解析收藏纠错 + 选题
8. (2020九上·渭滨期中) 如图，在Rt△ABC中，∠A=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为（）

A . 2 B . 2.2 C . 2.4 D . 2.5

答案解析收藏纠错 + 选题
9. (2020九上·渭滨期中) 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 的交点，过点 $\text{[math]}$ 作射线分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．给出下列结论： $\text{[math]}$ ； $\text{[math]}$ C； $\text{[math]}$ 四边形 $\text{[math]}$ 的面积为正方形 $\text{[math]}$ 面积的 $\text{[math]}$ ； $\text{[math]}$ ．其中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2024九上·高州开学考) 已知 $\text{[math]}$ 是关于x的一元二次方程，则m可取的值是.

答案解析收藏纠错 + 选题
11. (2020九上·渭滨期中) 一个等腰三角形的底边长是6，腰长是一元二次方程 $\text{[math]}$ 的一根，则此三角形的周长是.

答案解析收藏纠错 + 选题
12. (2020九上·渭滨期中) 如图，在矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
13. (2020九上·渭滨期中) 如图，矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在边 $\text{[math]}$ 上，连接 $\text{[math]}$ ，将 $\text{[math]}$ 和 $\text{[math]}$ 分别沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 上的同一点，记为点F.若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

14. (2020九上·渭滨期中) 选择适当的方法解下列方程
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
15. (2020九上·渭滨期中) $\text{[math]}$ 在边长为1的正方形网格中如图所示.
1. （1）画出将 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位长度的 $\text{[math]}$
2. （2）以点C为位似中心，作出 $\text{[math]}$ 的位似图形 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 位似比为 $\text{[math]}$ .且 $\text{[math]}$ 与 $\text{[math]}$ 位于点C的两侧，并表示出点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
16. (2020九上·渭滨期中) 已知：关于x的方程 $\text{[math]}$ 是否存在实数m，使方程的两个实数根的平方和等于 $\text{[math]}$ ？若存在，请求出满足条件的m值；若不存在，请说明理由.

答案解析收藏纠错 + 选题
17. (2022九下·余杭开学考) 随着“新冠肺炎”疫情防控形势日渐好转，各地开始复工复学，某校复学后成立“防疫志愿者服务队”，设立四个“服务监督岗”：①洗手监督岗，②戴口罩监督岗，③就餐监督岗，④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作，学校将报名的志愿者随机分配到四个监督岗.
1. （1）李老师被分配到“洗手监督岗”的概率为
2. （2）用列表法或面树状图法，求李老师和王老师被分配到同一个监督岗的概率.
答案解析收藏纠错 + 选题
18. (2020九上·渭滨期中)
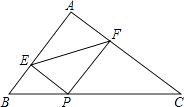
晚饭后，小聪和小军在社区广场散步，小聪问小军：“你有多高？”小军一时语塞．小聪思考片刻，提议用广场照明灯下的影长及地砖长来测量小军的身高．于是，两人在灯下沿直线NQ移动，如图，当小聪正好站在广场的A点（距N点5块地砖长）时，其影长AD恰好为1块地砖长；当小军正好站在广场的B点（距N点9块地砖长）时，其影长BF恰好为2块地砖长．已知广场地面由边长为0.8米的正方形地砖铺成，小聪的身高AC为1.6米，MN⊥NQ，AC⊥NQ，BE⊥NQ．请你根据以上信息，求出小军身高BE的长．（结果精确到0.01米）

答案解析收藏纠错 + 选题
19. (2024八下·丰城期中) 已知关于x的一元二次方程(a＋c)x²＋2bx＋(a－c)＝0，其中a ， b ， c分别为△ABC三边的长．
1. （1）如果x＝－1是方程的根，试判断△ABC的形状，并说明理由；
2. （2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．
答案解析收藏纠错 + 选题
20. (2020九上·渭滨期中) 如图，在菱形ABCD中，AB＝3，∠DAB＝60°，点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.
1. （1）求证：四边形AMDN是平行四边形；
2. （2）填空：①当AM的值为时，四边形AMDN是矩形；
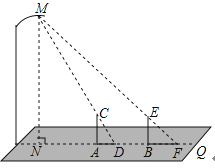
  ②当AM的值为时，四边形AMDN是菱形.
答案解析收藏纠错 + 选题
21. (2020九上·渭滨期中) 某商店销售甲、乙两种商品，现有如下信息：
请结合以上信息，解答下列问题：
1. （1）求甲、乙两种商品的进货单价；
2. （2）已知甲、乙两种商品的零售单价分别为2元、3元，该商店平均每天卖出甲商品500件和乙商品1300件，经市场调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件，商店决定把甲种商品的零售单价下降m（m＞0）元，在不考虑其他因素的条件下，求当m为何值时，商店每天销售甲、乙两种商品获取的总利润为1800元（注：单件利润=零售单价﹣进货单价）
答案解析收藏纠错 + 选题
22. (2022九上·渠县期末) 如图所示，在等腰△ABC中，AB＝AC＝10cm，BC＝16cm．点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s．连接DE，设运动时间为t（s）（0＜t＜10），解答下列问题：
1. （1）当t为何值时，△BDE的面积为7.5cm²；
2. （2）在点D，E的运动中，是否存在时间t，使得
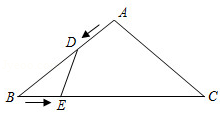
  △BDE与△ABC相似？若存在，请求出对应的时间t；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2020九上·渭滨期中) 如果关于x的一元二次方程 $\text{[math]}$ 有两个实数根，且其中一个根比另一个根大1，那么称这样的方程为“邻根方程”.例如，一元二次方程 $\text{[math]}$ 的两个根是 $\text{[math]}$ ，则方程 $\text{[math]}$ 是“邻根方程”.
1. （1）通过计算，判断下列方程是否是“邻根方程”：① $\text{[math]}$ ；② $\text{[math]}$
2. （2）已知关于x的方程 $\text{[math]}$ (m是常数)是“邻根方程”，求m的值.
答案解析收藏纠错 + 选题
24. (2020九上·渭滨期中)
1. （1）（操作发现）
  如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝45°，连接AC，BD交于点M.
  
  ①AC与BD之间的数量关系为；
  
  ②∠AMB的度数为；
2. （2）（类比探究）
  如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M.请计算 $\text{[math]}$ 的值及∠AMB的度数；
3. （3）（实际应用）
  如图（3），是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形，其中∠ACB＝∠DCE＝90°，∠A＝∠D＝30°且D、E、B在同一直线上，CE＝1，BC＝ $\text{[math]}$ ，求点A、D之间的距离.
答案解析收藏纠错 + 选题