浙江省湖州市吴兴区2020-2021学年八年级上学期数学期中...

更新时间：2024-07-13 浏览次数：241 类型：期中考试

一、选择题（本题有10小题，每小题3分，共30分）

1. (2020八上·吴兴期中) 2020年湖州市全面推行生活垃圾分类．下面图标分别为厨余垃圾、可回收物、有害垃圾、其他垃圾，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八上·义乌月考) 对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（）

A . ∠1=50°，∠2=40° B . ∠1=50°，∠2=50° C . ∠1=∠2=45° D . ∠1=40°，∠2=40°

答案解析收藏纠错 + 选题
3. (2024八上·蛟河期末) 下列各图中，正确画出AC边上的高的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020八上·吴兴期中) 若等腰三角形腰长是4，则底边不可能是（）

A . 1 B . 3 C . 6 D . 9

答案解析收藏纠错 + 选题
5. (2020八上·吴兴期中) 如图，是用直尺和圆规作一个角等于已知角的示意图，则说明 $\text{[math]}$ 的依据是（）

A . SAS B . SSS C . AAS D . ASA

答案解析收藏纠错 + 选题
6. (2020八上·吴兴期中) 如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，BD平分∠ABC ， P点是BD的中点，若AD＝6，则CP的长为（）

A . 3 B . 3.5 C . 4 D . 4.5

答案解析收藏纠错 + 选题
7. (2020八上·吴兴期中) “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC＝CD＝DE，点D、E可在槽中滑动.若∠BDE＝75°，则∠CDE的度数是（）

A . 90° B . 80° C . 70° D . 60°

答案解析收藏纠错 + 选题
8. (2020八上·吴兴期中) 如图，在△ABC中，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是（）

A . 5 B . 6 C . 4 D . 4.8

答案解析收藏纠错 + 选题
9. (2020八上·吴兴期中) 如图，等腰Rt△ABC中，∠ABC＝90°，O是△ABC内一点，OA＝6，OB＝ $\text{[math]}$ ，OC＝10， $\text{[math]}$ 为△ABC外一点，且△ $\text{[math]}$ ≌△ $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积为（）

A . 10 B . 16 C . 40 D . 80

答案解析收藏纠错 + 选题
10. (2023八上·余姚期中) △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）

A . △ABC的周长 B . △AFH的周长 C . 四边形FBGH的周长 D . 四边形ADEC的周长

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2021八上·兰溪期中) 在 $\text{[math]}$ 中，锐角∠A＝25°，则另一个锐角∠B＝°.

答案解析收藏纠错 + 选题
12. (2023八上·嘉兴月考) ”两个全等的三角形的周长相等“的逆命题是命题。（填”真“或”假“）。

答案解析收藏纠错 + 选题
13. (2020八上·吴兴期中) 如图，△ABC中，∠ABC，∠ACB的平分线相交于O，过点O作MN // BC，分别交AB、AC于点M、N.已知AB=5，AC=4，则△AMN的周长为.

答案解析收藏纠错 + 选题
14. (2020八上·吴兴期中) 如图，在等腰三角形ABC中，BC＝3 cm，△ABC的面积是9 cm² ，腰AB的垂直平分线EF交AC于点F，若点D为BC边上的中点，M为EF上的动点，则BM+DM的最小值为.

答案解析收藏纠错 + 选题
15. (2020八上·吴兴期中) 如图，已知△ABC，AB＝5，∠ABC＝60°，D为BC边上的点，AD＝AC，BD＝2，则DC＝.

答案解析收藏纠错 + 选题
16. (2020八上·吴兴期中) 如图，把一张长方形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BE＝BF＝1，则AB的长度为.

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共66分）

17. (2020八上·吴兴期中) 如图，在Rt△ABC中，∠ACB＝90°.
1. （1）用尺规在边BC上求作一点P，使PA＝PB（不写作法，保留作图痕迹）；
2. （2）连结AP，若AC＝6，BC＝8时，求△ACP的周长.
答案解析收藏纠错 + 选题
18. (2020八上·吴兴期中) 图①和图②是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的长均为1．请分别画出符合要求的图形，所画图形的各顶点必须与方格纸中的小正方形的顶点重合．
1. （1）请在图①中出一个面积为3的等腰三角形；
2. （2）请在图②中画出一个与△ABC全等的三角形ABD ．
答案解析收藏纠错 + 选题
19. (2020八上·吴兴期中) 如图，在等腰直角三角形ABC中，∠ABC＝90°，D，E在斜边AC上，且AD＝EC，连结BD，BE.若∠DBE＝50°，求∠BDE的度数.

答案解析收藏纠错 + 选题
20. (2020八上·吴兴期中) 如图，△ABC、△ADE中，C、D两点分别在AE、AB上，BC与DE相交于F点，且BD＝CD＝CE.
1. （1）若∠B=30°，∠E＝20°，求∠A的度数；
2. （2）若∠B=x，∠E＝y，请用含x、y的代数式表示∠A的度数.
答案解析收藏纠错 + 选题
21. (2023八上·长岭期中) 如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O.
1. （1）求证：△AEC≌△BED；
2. （2）若∠1＝48°，求∠BDE的度数.
答案解析收藏纠错 + 选题
22. (2020八上·吴兴期中) 如图，△ABC中，∠C＝90°，AC＝4厘米，BC＝3厘米，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1厘米，设运动的时间为t秒．
1. （1）当t为何值时，CP把△ABC的周长分成相等的两部分．
2. （2）当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；
3. （3）当t为何值时，△BCP为等腰三角形？
答案解析收藏纠错 + 选题
23. (2020八上·吴兴期中) 如图
1. （1）【问题探究】
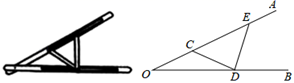
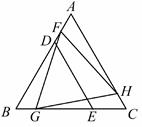
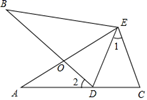
  如图①，锐角△ABC中，分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD ，使AE＝AB ， AD＝AC ， ∠BAE＝∠CAD＝90°，连接BD ， CE ，试猜想BD与CE的大小关系，不需要证明．
2. （2）【深入探究】
  如图②，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD ，使AE＝AB ， AD＝AC ， ∠BAE＝∠CAD ，连接BD、CE ，试猜想BD与CE的大小关系，并说明理由．
3. （3）【拓展应用】
  如图③，在△ABC中，∠ACB=45°，以AB为直角边，A为直角顶点向外作等腰直角△ABD ，连接CD ，若AC= $\text{[math]}$ ，BC=3，则CD长为．
答案解析收藏纠错 + 选题
24. (2020八上·吴兴期中) 具有公共顶点A的△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，连结BD，CE.
1. （1）如图①，当∠EAC=度时，△AEC≌△ADB；
2. （2）如图②，保持△ABC的位置不变，将△ADE绕点A顺时针方向旋转，连结BD，CE.此时△AEC和△ADB的面积相等吗？请你作出判断，并说明理由；
3. （3）请你运用探索到的结论解决以下问题：
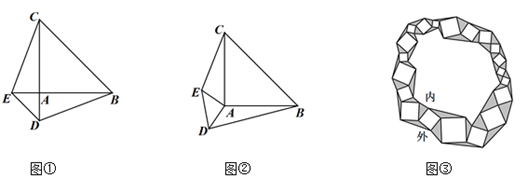
  如图③，一条环形小路是由白色的正方形大理石和花色的三角形大理石铺成的.已知小路的总面积为（a²+b²）平方米，中间的所有正方形的面积之和为（2a+4b-9）平方米，内圈的所有三角形的面积之和为（a+b-2）平方米，求a，b的值.
答案解析收藏纠错 + 选题