浙江省诸暨市暨阳初中教育共同体2020-2021学年八年级上...

更新时间：2024-07-13 浏览次数：280 类型：期中考试

一、单选题

1. (2020八上·诸暨期中) 在以下节能、节水、绿色食品、回收四个标志中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八上·西湖期中) 下列语句是命题的是（）

A . 作直线AB的垂线 B . 在线段AB上取点C C . 同旁内角互补 D . 垂线段最短吗？

答案解析收藏纠错 + 选题
3. (2020八上·诸暨期中) 在下列条件中，不能说明△ABC≌△A’B’C^’的是（）

A . ∠A＝∠A’，∠C＝∠C’，AC＝A’C’ B . ∠A＝∠A’，AB＝A’B’，BC＝B’C’ C . ∠B＝∠B’，∠C＝∠C’，AB＝A’B’ D . AB＝A’B’， BC＝B’ C’，AC＝A’C’

答案解析收藏纠错 + 选题
4. (2020八上·诸暨期中) 已知a＜b，下列不等式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ a﹣3＜ $\text{[math]}$ b﹣3 C . a+3＞b+3 D . ﹣3a＜﹣3b

答案解析收藏纠错 + 选题
5. (2020八上·诸暨期中) 若等腰三角形的两边长分别是4和9，则它的周长是（）

A . 17 B . 13 C . 17或22 D . 22

答案解析收藏纠错 + 选题
6. 在直角三角形ABC中，∠A：∠B：∠C＝2：m：4，则m的值是（）

A . 3 B . 4 C . 2或6 D . 2或4

答案解析收藏纠错 + 选题
7. (2020八上·诸暨期中) 如图，已知直线1交直线a，b于A，B两点，且a∥b，E是a上的点，F是b上的点，满足∠DAE= $\text{[math]}$ ∠BAE，∠DBF= $\text{[math]}$ ∠ABF，则∠ADB的度数是（）

A . 45° B . 50° C . 60° D . 无法确定

答案解析收藏纠错 + 选题
8. (2023七下·上海市期末) 如图，已知AB=AC=BD，那么∠1与∠2之间的关系是（）

A . ∠1=2∠2 B . 2∠1+∠2=180° C . ∠1+3∠2=180° D . 3∠1-∠2=180°

答案解析收藏纠错 + 选题
9. (2020八上·诸暨期中) 如图，以Rt△ABC的三条边作三个正三角形，则S₁、S₂、S₃、S₄的关系为（）

A . S₁+S₂+S₃＝S₄ B . S₁+S₂＝S₃+S₄ C . S₁+S₃＝S₂+S₄ D . 不能确定

答案解析收藏纠错 + 选题
10. (2020八上·诸暨期中) 如图，∠AOB=45°，∠AOB内有一定点P，且OP=8.在OA上有一动点Q，OB上有一动点R.若△PQR周长最小，则最小周长是（）

A . 8 B . $\text{[math]}$ C . 16 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023八上·鄞州期末) 根据数量关系列不等式： $\text{[math]}$ 的2倍与 $\text{[math]}$ 的差大于3.

答案解析收藏纠错 + 选题
12. (2023八上·瓯海期中) 命题“等腰三角形两底角相等”的逆命题是。

答案解析收藏纠错 + 选题
13. (2020八下·新城期末) Rt△ABC中∠ABC=90°，斜边AC=10cm，D为斜边上的中点，斜边上的中线BD=.

答案解析收藏纠错 + 选题
14. (2024八上·海安月考) 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为．

答案解析收藏纠错 + 选题
15. (2020八上·诸暨期中) 如图，在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E，F，连结CE，BF.添加一个条件，使得△BDF≌△CDE，你添加的条件是（不添加辅助线）.

答案解析收藏纠错 + 选题
16. (2020八上·诸暨期中) 如图，已知△ABC中，AD是BC边上的高，AE是∠BAC的平分线，若∠B=65°，∠C=45°，则∠DAE的度数为.

答案解析收藏纠错 + 选题
17. (2020八上·诸暨期中) 如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，AC=12cm，则△APC的面积是

答案解析收藏纠错 + 选题
18. (2020八上·诸暨期中) 把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF.若AB=6cm，BC=10cm，则AE= cm.

答案解析收藏纠错 + 选题
19. (2020八上·诸暨期中) 如图，在△ABC中，已知点D为BC上一点，E，F分别为AD，BE的中点，且S_△_ABC=13，则图中阴影部分△CEF的面积是.

答案解析收藏纠错 + 选题
20. (2021八下·太和期中) 如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，以点B为旋转中心，将线段BO逆时针旋转60°得到线段BO′，连接AO′.则下列结论：

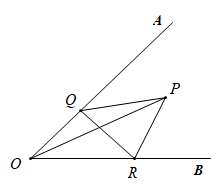
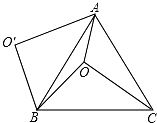
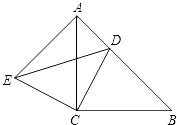
①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到；

②连接OO′，则OO′=4；

③∠AOB=150°；

④S_{四边形AOBO′}=6+4 $\text{[math]}$ .

其中正确的结论是.

答案解析收藏纠错 + 选题

三、解答题

21. (2020八上·诸暨期中) 已知：如图，∠C=∠D=90°，AD=BC.求证：∠ABC=∠BAD.

答案解析收藏纠错 + 选题
22. (2020八上·诸暨期中) 如图，在△ABC中，∠C=90°，边AB的垂直平分线交AB，AC边分别为点D，点E，连结BE.
1. （1）若∠A=35°，求∠CBE的度数；
2. （2）若AB=10，BC=6，求△BCE的周长.
答案解析收藏纠错 + 选题
23. (2022八下·定远期中) 如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：
1. （1） △ACE≌△BCD；
2. （2） AD²+DB²=DE² ．
答案解析收藏纠错 + 选题
24. (2020八上·诸暨期中) 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点.
1. （1）特例感知
  ①等腰直角三角形勾股高三角形（请填写“是”或者“不是”）；
  
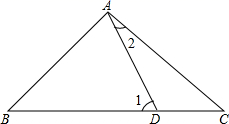
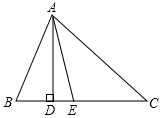
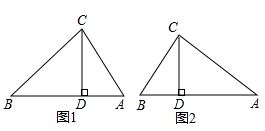
  ②如图1，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高.若BD=2，AD=1，试求线段CD的长度.
2. （2）深入探究
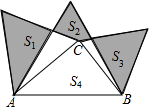
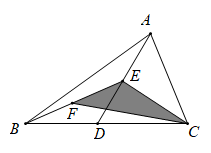
  如图2，已知△ABC为勾股高三角形，其中C为勾股顶点且CA>CB，CD是AB边上的高.试探究线段AD与CB的数量关系，并给予证明.
答案解析收藏纠错 + 选题
25. (2020八上·诸暨期中) 如图，在Rt△ABC中，AB=8，BC=6，点D从B点出发，沿射线CB方向以每秒3个单位长度的速度运动，射线MP⊥射线CB且BM=10，点Q从M点出发，沿射线MP方向以每秒a个单位长度的速度运动，已知D、Q两点同时出发，运动时间为t秒.
1. （1）当t=2时，△DMQ是等腰三角形，求a的值.
2. （2）求t为何值时，△DCA为等腰三角形.
3. （3）是否存在a，使得△DMQ与△ABC全等，若存在，请直接写出a的值，若不存在，请说明理由
答案解析收藏纠错 + 选题
26. (2020八上·诸暨期中) 如图1，等边△ABC边长为8，AD是△ABC的中线，P为线段AD（不包括端点A、D）上一动点，以CP为一边且在CP下方作如图所示的等边△CPE，连结BE.
1. （1）点P在运动过程中，线段BE与AP始终相等吗？说说你的理由
2. （2）若延长BE至F，使得CF=CE=5，如图2，
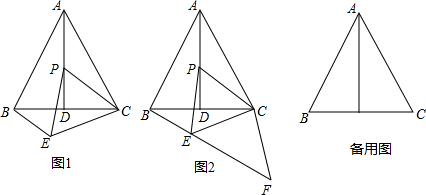
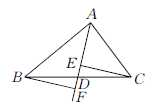
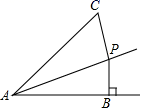
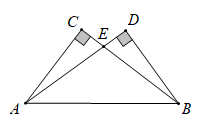
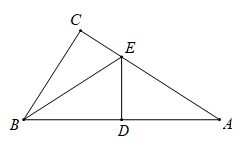
  ①求出此时AP的长；
  
  ②当点P在线段AD的延长线上，点F在射线BE上时，判断EF的长是否为定值，若是请直接写出EF的长；若不是请简单说明理由.
答案解析收藏纠错 + 选题