江苏省宿迁市钟吾初级中学2020-2021学年八年级上学期数...

更新时间：2024-07-31 浏览次数：215 类型：期中考试

一、单选题

1. (2023八上·铁锋期末) 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九下·滨海模拟) 估计 $\text{[math]}$ 的值在（）

A . 1和2之间 B . 2和3之间 C . 3和4之间 D . 4和5之间

答案解析收藏纠错 + 选题
3. (2023八上·翠屏期末) 下列长度的三条线段能组成直角三角形的是（）

A . 3，4，5 B . 2，3，4 C . 4，6，7 D . 5，11，12

答案解析收藏纠错 + 选题
4. (2020八上·宿迁期中) 若等腰三角形中有两边长分别为2和3，则这个三角形的周长为（）

A . 7 B . 7或8 C . 8 D . 9或7

答案解析收藏纠错 + 选题
5. (2020八上·宿迁期中) 如图所示，在下列条件中，不能判断△ABD≌△BAC的条件是（）

A . ∠D＝∠C，∠BAD＝∠ABC B . ∠BAD＝∠ABC，∠ABD＝∠BAC C . BD＝AC，∠BAD＝∠ABC D . AD＝BC，BD＝AC

答案解析收藏纠错 + 选题
6. (2020八上·宿迁期中) 如图，小敏用三角尺按下面方法画角平分线：在已知的∠AOB的两边上，分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB，其作图原理是：△OMP≌△ONP，这样就有∠AOP＝∠BOP，则说明这两个三角形全等的依据是（）

A . SAS B . ASA C . AAS D . HL

答案解析收藏纠错 + 选题
7. (2023八下·景县期中) 在Rt△ABC中，∠B＝90°，BC＝1，AC＝2，则AB的长是（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020八上·宿迁期中) 如图，长方形纸片ABCD中，AB＝4，BC＝6，点E在AB边上，将纸片沿CE折叠，点B落在点F处，EF，CF分别交AD于点G，H，且EG＝GH，则AE的长为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题

二、填空题

9. (2024七下·重庆市期中) 实数8的立方根是．

答案解析收藏纠错 + 选题
10. (2024八下·沈阳期中) 如果等腰三角形有一个内角为110°，则其底角的度数是.

答案解析收藏纠错 + 选题
11. (2020八上·宿迁期中) 若直角三角形斜边上的中线为10 cm，则它的斜边长是cm.

答案解析收藏纠错 + 选题
12. (2022八下·南充期末) 已知等腰ΔABC中，AB＝AC＝5，BC＝6，则ΔABC的面积为.

答案解析收藏纠错 + 选题
13. (2020八上·宿迁期中) 如图，线段AB//CD，且CE＝BF，请添加一个适当的条件使ΔABF≌ΔDCE.（只填一个即可）

答案解析收藏纠错 + 选题
14. (2020八上·宿迁期中) 如图，在等边 $\text{[math]}$ 中，D、E分别是边AB、AC上的点，且 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2020八上·宿迁期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2020八上·宿迁期中) 如图，△ABC中，∠C＝90°，AD是角平分线，若CD＝2，则点D到AB的距离等于.

答案解析收藏纠错 + 选题
17. (2020八上·宿迁期中) 如图，已知ΔABC中，PM、QN分别是AB，AC边上的垂直平分线，∠BAC＝100°，AB＞AC，则∠PAQ的度数是.

答案解析收藏纠错 + 选题
18. (2020八上·宿迁期中) 如图，已知点B在数轴负半轴上，O为原点，点A在过O且垂直于数轴的直线上，∠BAO＝60°，AB＝4，点C在数轴上，当ΔABC是以AB为腰的等腰三角形时，点C表示的数为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020八上·宿迁期中) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2020八上·宿迁期中) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2020八上·宿迁期中) 已知 $\text{[math]}$ 的算术平方根是3， $\text{[math]}$ 的算术平方根是4，c是 $\text{[math]}$ 的整数部分，求 $\text{[math]}$ 的立方根.

答案解析收藏纠错 + 选题
22. (2020八上·宿迁期中) 如图，已知CD⊥AB，CD＝2，BD＝4，AD＝1，求证：∠ACB是直角.

答案解析收藏纠错 + 选题
23. (2020八上·宿迁期中) 已知点C和点F在线段BE上，且AB＝DE，∠B＝∠E，BC＝EF，AC和DF相交于点G.
1. （1）求证：△ABC≌△DEF；
2. （2）当∠AGF＝120°，猜想△GFC的形状，并说明理由.
答案解析收藏纠错 + 选题
24. (2020八上·宿迁期中) 如图，在边长为1个单位长度的小正方形网格纸中，格线与格线的交点称为格点，以格点为顶点的三角形称为格点三角形，ΔABC就是一个格点三角形.

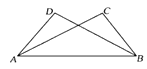
（ 1 ）请画出ΔABC关于直线 $\text{[math]}$ 对称的格点ΔA₁B₁C₁；

（ 2 ）请用无刻度的直尺，借助网格作出ΔABC的AC边上的中线；

（ 3 ）将线段AC向左平移3个单位长度，再向下平移5个单位长度，画出平移后得到的线段A₂C₂ ，并以它为一边作格点ΔA₂B₂C₂ ，使得A₂B₂＝C₂B₂ ，满足条件的格点B₂共有个.

答案解析收藏纠错 + 选题
25. (2020八上·宿迁期中) 如图①，ΔABC中，∠B、∠C的平分线交于O点，过O点作EF//BC分别交AB、AC于E，F.
1. （1）猜想：EF与BE、CF之间有怎样的关系.并说明理由.
2. （2）如图②，若ΔABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE//BC交AB于E，交AC于F.这时图中EF与BE、CF关系又如何？说明你的理由.
答案解析收藏纠错 + 选题
26. (2021八上·南昌期末) 某班级在探究“将军饮马问题”时抽象出数学模型：
直线 $\text{[math]}$ 同旁有两个定点A、B，在直线 $\text{[math]}$ 上存在点P，使得PA十PB的值最小.解法：如图1，作点A关于直线 $\text{[math]}$ 的对称点A'，连接A'B，则A'B与直线 $\text{[math]}$ 的交点即为P，且PA＋PB的最小值为A'B.

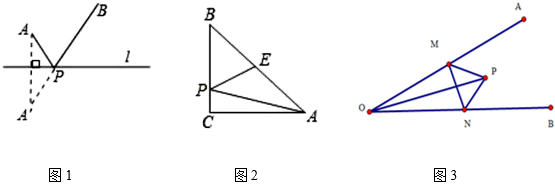
请利用上述模型解决下列问题；
1. （1）如图2，ΔABC中，∠C=90°，E是AB的中点，P是BC边上的一动点，作出点P，使得PA＋PE的值最小；
2. （2）如图3，∠AOB=30°，M、N分别为OA、OB上一动点，若OP=5，求ΔPMN的周长的最小值.
答案解析收藏纠错 + 选题
27. (2020八上·宿迁期中) 已知，如图，在ΔABC与ΔADE中，AB=AC，AD=AE，
1. （1）如图①，连接CD、BE，交于G点，若∠BAC=∠DAE= $\text{[math]}$ ，求∠BGC度数.
2. （2）如图②，连接CE、BD，若P为BD中点，且∠EAC=∠ABD＋∠ADB，试探究AP与CE的数量关系，并说明理由.
答案解析收藏纠错 + 选题
28. (2020八上·宿迁期中) （数学实验）小明在学习轴对称一章角平分线一节后，做了一个实验：
第一步：如图1在一张纸上画了一个平角∠AOB；

第二步：如图2在平角∠AOB内画一条射线，沿着射线将平角∠AOB裁开；

第三步：如图3将∠AO'C'放在∠COB内部，使两边分别与OB、OC相交，且O'A＝O'C'；

第四步：连接OO'，测量∠COB度数和∠COO'度数.

（数学发现与证明）通过以上实验，小明发现OO'平分∠COB. 你能根据小明的实验给出的条件：
1. （1） ∠AO'C'与∠COB的关系是；
2. （2）线段O'A与O'C'的关系是 ▲ .
  请您结合图3将小明的实验条件和发现结论完成下面“已知”“求证”，并给出证明.
  
  已知：
  
  求证：
  
  证明：
答案解析收藏纠错 + 选题