浙江省宁波市象山文峰学校2020-2021学年九年级上学期数...

更新时间：2021-01-15 浏览次数：239 类型：月考试卷

一、单选题

1. (2020九上·象山月考) 下列说法中错误的是（）

A . 0的相反数是0 B . 任何有理数都有相反数 C . a 的相反数是-a D . 表示相反意义的量的两个数互为相反数

答案解析收藏纠错 + 选题
2. (2020九上·象山月考) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·象山月考) PM2.5 是指大气中直径小于或等于 2.5 微米的颗粒物，2.5 微米等于 0.000 002 5 米，把0.0000025 用科学记数法表示为（）

A . 2.5×10 ^-6 B . 0.25×10 ^-5 C . 2.5×10 ⁶ D . 25×10 ^-7

答案解析收藏纠错 + 选题
4. (2024·广东模拟) 如图是由4个相同的正方体搭成的几何体，则其俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021九上·邗江期末) 某篮球运动员在连续7场比赛中的得分（单位：分）依次为20，18，23，17，20，20，18，则这组数据的众数与中位数分别是（）

A . 18分，17分 B . 20分，17分 C . 20分，19分 D . 20分，20分

答案解析收藏纠错 + 选题
6. (2020九上·象山月考) 在平面直角坐标系中，已知，设函数的图象与 a≠b， y = (x + a)(x + b) x 轴有M个交点，函数y = (ax +1)(bx +1)的图像与x轴有N个交点，则（）

A . M=N-1或M = N+1 B . M=N-1或M=N+2 C . M=N或M=N+1 D . M=N或M= N-1

答案解析收藏纠错 + 选题
7. (2021九上·余杭期末) 如图，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·象山月考) 如图，在△ABC 中，D、E分别是AB、BC上的点，且DE∥AC，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值（）

A . 1∶5 B . 1∶9 C . 1∶12 D . 1∶16

答案解析收藏纠错 + 选题
9. (2020九上·象山月考) 复习课中，教师给出关于x的函数y=﹣2mx+m﹣1（m≠0）．学生们在独立思考后，给出了5条关于这个函数的结论：
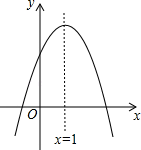
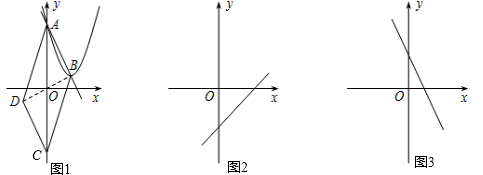
①此函数是一次函数，但不可能是正比例函数；
②函数的值y 随着自变量x的增大而减小；
③该函数图象与y轴的交点在y轴的正半轴上；
④若函数图象与x轴交于A（a，0），则a＜0.5；
⑤此函数图象与直线y=4x﹣3、y轴围成的面积必小于0.5．
对于以上5个结论是正确有（）个．

A . 4 B . 3 C . 2 D . 0

答案解析收藏纠错 + 选题
10. (2020九上·象山月考) 如图，在轴正半轴上依次截取 $\text{[math]}$ ，过点 $\text{[math]}$ 分别作x轴的垂线，与反比例函数 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ 过点 $\text{[math]}$ 分别向 $\text{[math]}$ 作垂线段，构成的一系列直角三角形（图中阴影部分）的面积和等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·象山月考) 写出－2和0之间的一个无理数：.

答案解析收藏纠错 + 选题
12. (2020九上·象山月考) 分解因式：x²﹣9x=．

答案解析收藏纠错 + 选题
13. (2020九上·象山月考) 计算 $\text{[math]}$ 的结果是；分式方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
14. (2020九上·象山月考) 一个扇形的圆心角为 120°，半径为 2，则这个扇形的弧长为.

答案解析收藏纠错 + 选题
15. (2020九上·象山月考) 如图，抛物线y＝ax²+bx+c与x轴交于点A(﹣1，0)，顶点坐标为C(1，k)，与y轴的交点在(0，2)、(0，3)之间（不包含端点），则k的取值范围是.

答案解析收藏纠错 + 选题
16. (2021九上·余杭期末) 如图，在矩形 ABCD 中，AB=2，BC=4，⊙D 的半径为 1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为 .

答案解析收藏纠错 + 选题

三、解答题

17. (2020九上·象山月考) 计算：
1. （1）计算： $\text{[math]}$
2. （2）计算 $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020九上·象山月考) 如图，在平面直角坐标系中，已知的三个顶点的坐标分别为 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 和 $\text{[math]}$ 关于x轴成轴对称，画出 $\text{[math]}$
2. （2）点C₁的坐标为， $\text{[math]}$ 的面积为．
答案解析收藏纠错 + 选题
19. (2020九上·象山月考) 如图，某市郊外景区内一条笔直的公路l经过A、B两个景点，景区管委会又开发了风景优美的景点C．经测量，C位于A的北偏东60°的方向上，C位于B的北偏东30°的方向上，且AB=10km．
1. （1）求景点B与C的距离；
2. （2）为了方便游客到景点C游玩，景区管委会准备由景点C向公路l修一条距离最短的公路，不考虑其他因素，求出这条最短公路的长．（结果保留根号）
答案解析收藏纠错 + 选题
20. (2021九下·松山期中) 已知：如图，在△ABC 中，AB＝AC，AE是角平分线，BM平分∠ABC交AE于点 M，经过B，M两点的 ⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
1. （1）求证：AE与⊙O相切；
2. （2）当 BC＝4，AC＝6，求⊙O 的半径．
答案解析收藏纠错 + 选题
21. (2020九上·象山月考) 为响应国家的“一带一路”经济发展战略，树立品牌意识，我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测，通过检测得出C厂家的合格率为95%，并根据检测数据绘制了如图1、图2两幅不完整的统计图．
1. （1）抽查D厂家的零件为件，扇形统计图中D厂家对应的圆心角为；
2. （2）抽查C厂家的合格零件为件，并将图1补充完整；
3. （3）通过计算说明合格率排在前两名的是哪两个厂家；
4. （4）若要从A、B、C、D四个厂家中，随机抽取两个厂家参加德国工业产品博览会，请用“列表法”或“画树形图”的方法求出（3）中两个厂家同时被选中的概率．
答案解析收藏纠错 + 选题
22. (2020九上·象山月考) 某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现，当销售单价是25 元时，每天的销售量为 250 件；销售单价每上涨1元，每天的销售量就减少10件．
1. （1）写出商场销售这种文具每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；
2. （2）商场的营销部结合上述情况，提出了A、B两种营销方案：方案A：该文具的销售单价高于进价且不超过30元；方案B：每天销售量不少于10件，且每件文具的利润至少为25元．请比较哪种方案的最大利润更高，并说明理由．
答案解析收藏纠错 + 选题
23. (2020九上·象山月考) 如图，已知tan∠EOF=2，点C在射线OF上，OC=12．点M是∠EOF内一点，MC⊥OF于点C，MC=4．在射线CF上取一点A，连结AM并延长交射线OE于点B，作BD⊥OF于点D．
1. （1）当AC的长度为多少时，△AMC和△BOD相似；
2. （2）当点M恰好是线段AB中点时，试判断△AOB的形状，并说明理由；
3. （3）连结BC．当S_△_AMC=S_△_BOC时，求AC的长．
答案解析收藏纠错 + 选题
24. (2020九上·象山月考) 已知抛物线 y＝a(x－m)²＋n与y轴交于点A，它的顶点为点B，点A、B关于原点O的对称点分别为C、D．若A、B、C、D中任何三点都不在一直线上，则称四边形ABCD为抛物线的伴随四边形，直线AB为抛物线的伴随直线．
1. （1）如图1，求抛物线y＝(x－2)²＋1的伴随直线的解析式．
2. （2）如图2，若抛物线y＝a(x－m)²＋n(m＞0)的伴随直线是y＝x－3，伴随四边形的面积为 12，求此抛物线的解析式．
3. （3）如图3，若抛物线y＝a(x－m)²＋n 的伴随直线是y＝－2x＋b(b＞0)，且伴随四边形ABCD是矩形．
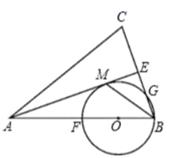
  ①用含b的代数式表示m、n的值；
  
  ②在抛物线的对称轴上是否存在点P，使得△PBD是一个等腰三角形？若存在，请直接写出点P的坐标(用含b的代数式表示)，若不存在，请说明理由．
答案解析收藏纠错 + 选题