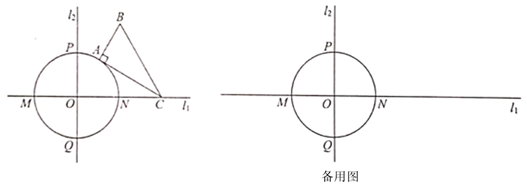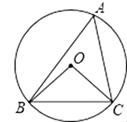
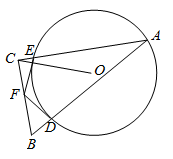
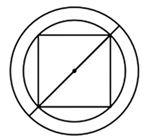
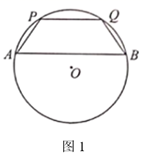
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为尺.(结果用最简根式表示)
|
售价 | 200 | 240 | 250 | 400 |
| 销售量 | 30 | 25 | 24 | 15 |
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为元.
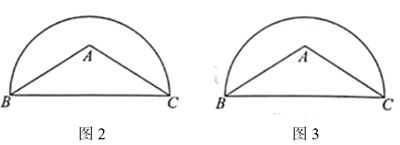
①在图2中,作弦 ,使
;
②在图3中,以 为边作一个
的圆周角.

根据上面的定义和提示,解答下列问题:
②在如图所示的平面直角坐标系中画出 的“反函数”的大致图象;