河北省衡水市景县第二中学2020-2021学年八年级上学期数...

更新时间：2024-07-31 浏览次数：202 类型：期中考试

一、填空题

1. (2020八上·景县期中) 如图， $\text{[math]}$ 要使 $\text{[math]}$ ，还需添加一个条件是（填上适当的一个条件即可）．

答案解析收藏纠错 + 选题
2. (2020八上·景县期中)
如图，△ABC≌△ADE ， ∠EAC=25°，则∠BAD= °.

答案解析收藏纠错 + 选题
3. (2020八上·景县期中) 若直角三角形的斜边长为 10 cm，则斜边上的中线长为cm.

答案解析收藏纠错 + 选题
4. (2020八上·景县期中) 在等腰三角形 $\text{[math]}$ 中，它的两边长分别为 $\text{[math]}$ 和 $\text{[math]}$ 则它的周长为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
5. (2020八上·景县期中) 如图所示，已知 $\text{[math]}$ 为 $\text{[math]}$ 的垂直平分线，则 $\text{[math]}$ 的度数为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
6. (2021八上·大埔期中) 若直角三角形的两直角边长分别为 $\text{[math]}$ ， $\text{[math]}$ ，则斜边的长为cm．

答案解析收藏纠错 + 选题
7. (2020八上·景县期中) 我们规定：等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”，记作 $\text{[math]}$ ．若 $\text{[math]}$ 则该等腰三角形的顶角为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. (2020八上·景县期中) 如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，DE＝2，BC＝5，则△BCE的面积为．

答案解析收藏纠错 + 选题
9. (2020八上·景县期中) 如图，AD是△ABC的中线，且∠ADC=60°，BC=4，把△ADC沿直线AD折叠后，点C落在点C'的位置上.则B C'=.

答案解析收藏纠错 + 选题
10. (2020八上·景县期中) 如图，点P为∠AOB内任一点，E，F分别为点P关于OA，OB的对称点．若∠AOB＝30°，则∠E＋∠F＝°．

答案解析收藏纠错 + 选题
11. (2022九下·北京市开学考) 如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAC+∠ACD＝°．

答案解析收藏纠错 + 选题
12. (2020八上·景县期中) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ 是对角线， $\text{[math]}$ 是等边三角形， $\text{[math]}$ 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

二、单选题

13. (2020八上·景县期中) 下列图形不一定是轴对称图形的是（）

A . 线段 B . 角 C . 等腰三角形 D . 直角三角形

答案解析收藏纠错 + 选题
14. (2020八上·景县期中) 下列条件中，不能判断 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2020·邯郸模拟) 如图，已知△ABC(AB＜BC＜AC)，用尺规在AC上确定一点P，使PB+PC＝AC，则下列选项中，一定符合要求的作图痕迹是（）

A . B . C . D .

答案解析收藏纠错 + 选题
16. (2020八上·景县期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 和 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，若 $\text{[math]}$ 则线段 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2020八上·景县期中) 一棵大树在一次强台风中于离地面 $\text{[math]}$ 米处折断倒下，倒下部分与地面成 $\text{[math]}$ 夹角，这棵大树在折断前的高度为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
18. (2020八上·景县期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 分别在 $\text{[math]}$ 上，且 $\text{[math]}$ 将 $\text{[math]}$ 沿 $\text{[math]}$ 所在的直线折叠得到 $\text{[math]}$ （点 $\text{[math]}$ 在四边形 $\text{[math]}$ 内），连接 $\text{[math]}$ 则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

19. (2020八上·景县期中) 已知：如图， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2020八上·景县期中) 如图，已知 $\text{[math]}$ 及点 $\text{[math]}$ 两点，求作一点 $\text{[math]}$ ，使得点 $\text{[math]}$ 到射线 $\text{[math]}$ 的距离相等，且点Р到点 $\text{[math]}$ 的距离也相等（要求尺规作图，不写作法，并保留作图痕迹）．

答案解析收藏纠错 + 选题
21. (2023八下·宁远期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过 $\text{[math]}$ 的中点D作 $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点E、F．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
22. (2020八上·景县期中) 如图， $\text{[math]}$ 于 $\text{[math]}$ 于 $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）试探究线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量和位置关系，并说明理由．
答案解析收藏纠错 + 选题
23. (2020八上·景县期中) 已知如图， $\text{[math]}$ ．求四边形 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
24. (2020八上·景县期中) 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B在小正方形的顶点上.
1. （1）在直线l上找一点C，使它到A，B两点的距离相等；
2. （2）在（1）的基础上画出△ABC关于直线l成轴对称的△A′B′C′；
3. （3）在直线l上找一点P（在答题纸上图中标出），使PA+PB的长最短，这个最短长度的平方值是．
答案解析收藏纠错 + 选题
25. (2020八上·景县期中) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ $\text{[math]}$ ．试说明：
1. （1）求证 $\text{[math]}$ ；
2. （2） $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
26. (2020八上·景县期中) （材料学习）
小学里已经学过：一组对边平行，另一组对边不平行的四边形称为梯形，平行的一组对边称为底，不平行的一组对边称为腰．

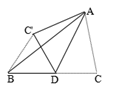
如图（1），在等腰三角形纸片 $\text{[math]}$ 上，画底边 $\text{[math]}$ 的平行线 $\text{[math]}$ 可得到一个梯形 $\text{[math]}$ ．由 $\text{[math]}$ $\text{[math]}$ 可知 $\text{[math]}$ ，于是 $\text{[math]}$ ，又 $\text{[math]}$ ，从而 $\text{[math]}$ ．

定义：像梯形 $\text{[math]}$ ，两腰相等的梯形称为等腰梯形．

几何语言：如图（1）， $\text{[math]}$ 在梯形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 梯形 $\text{[math]}$ 是等腰梯形．

如果把图（1）的等腰三角形纸片 $\text{[math]}$ 沿顶角平分线 $\text{[math]}$ 折叠，那么 $\text{[math]}$ 与 $\text{[math]}$ 重合，由于 $\text{[math]}$ ，可知点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，如图（）2，于是 $\text{[math]}$ ．由此，我们可以得到如下结论：

①等腰梯形是轴对称图形，过两底中点的直线是它的对称轴，

②等腰梯形在同一底上的两个角相等，

③等腰梯形的对角线相等．

（探究归纳）

利用等腰梯形与等腰三角形的内在联系，我们还可以研究：具备什么条件的梯形是等腰梯形?
1. （1）如图（3），在梯形 $\text{[math]}$ 中， $\text{[math]}$ ，求证：梯形 $\text{[math]}$ 是等腰梯形；
2. （2）通过（1）的证明可知：的梯形是等腰梯形；
3. （3）如图（4），在梯形 $\text{[math]}$ 中， $\text{[math]}$ ，求证：梯形 $\text{[math]}$ 是等腰梯形．
4. （4）通过（3）证明可知：的梯形是等腰梯形；
答案解析收藏纠错 + 选题
27. (2020八上·景县期中) 勾股定理是一个基本的几何定理，尽在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载．如果一个直角三角形三边长都是正整数，这样的直角三角形叫“整数直角三角形”，这三个整数叫做一组“勾股数”．如 $\text{[math]}$ $\text{[math]}$ ：等等都是勾股数．
1. （1）如果 $\text{[math]}$ 是一组勾股数，即满足 $\text{[math]}$ ，则 $\text{[math]}$ 为正整数）也是一组勾股数．如； $\text{[math]}$ 是一组勾股数，则也是一组勾股数；
2. （2）另外利用一些构成勾股数的公式也可以写出许多勾股数，毕达哥拉斯学派就曾提出 $\text{[math]}$ 公式为正整数）是一组勾股数，证明满足以上公式的 $\text{[math]}$ 是一组勾股数；
3. （3）值得自豪的是，世界上第一次给出的勾股数公式，收集在我国的《九章算术》中，书中提到：当 $\text{[math]}$ ， $\text{[math]}$ 为正整数， $\text{[math]}$ 时， $\text{[math]}$ 构成一组勾股数；请根据这一结论直接写出一组符合条件的勾股数．
4. （4）观察 $\text{[math]}$ ；…，可以发现这些勾股数的勾都是奇数，且从 $\text{[math]}$ 起就没有间断过，并且勾为 $\text{[math]}$ 时股 $\text{[math]}$ ，弦 $\text{[math]}$ ；勾 $\text{[math]}$ 为时，股 $\text{[math]}$ ，弦 $\text{[math]}$ ；
  请仿照上面两组样例，用发现的规律填空：
  
  ①如果勾为7，则股 $\text{[math]}$ ；弦 $\text{[math]}$ ；
  
  ②如果用 $\text{[math]}$ 且 $\text{[math]}$ 为奇数）表示勾，请用含有 $\text{[math]}$ 的式子表示股和弦，则股 $\text{[math]}$ ；弦 $\text{[math]}$ ；
  
  ③观察 $\text{[math]}$ ；…，可以发现各组的第一个数都是偶数，且从 $\text{[math]}$ 起也没有间断过．则 $\text{[math]}$ ；请你直接用 $\text{[math]}$ 为偶数且 $\text{[math]}$ ）的代数式表示直角三角形的另一条直角边；和弦的长．
答案解析收藏纠错 + 选题
28. (2020八上·景县期中) 倍长中线的思想在丁倍长某条线段（被延长的线段 $\text{[math]}$ 要满足两个条件： $\text{[math]}$ 线段 $\text{[math]}$ 一个端点是图中一条线段 $\text{[math]}$ 的中点； $\text{[math]}$ 线段 $\text{[math]}$ 与这条线段 $\text{[math]}$ 不共线），然后进行连接，构造三角形全等，再进一步将某些线段进行等量代换，再证明全等或其他的结论，从而解决问题．
1. （1）如图（1），已知： $\text{[math]}$ 为 $\text{[math]}$ 的中线，求证： $\text{[math]}$ ．
  
  简证：如图（2），延长 $\text{[math]}$ 到 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ，易证 $\text{[math]}$ ，得 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）如图（3），在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线， $\text{[math]}$ 是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，求证： $\text{[math]}$ ．
3. （3）如图（4），在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边的中点， $\text{[math]}$ 分别在边 $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
4. （4）如图（5）， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ ，且 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系及位置关系．
答案解析收藏纠错 + 选题