北京市第四中学2021-2022学年九年级下学期数学开学测试...

更新时间：2024-07-31 浏览次数：99 类型：开学考试

一、单选题

1. (2024九下·廉江模拟) 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食物和药物，得到广泛的使用．经测算，一粒芝麻的质量约为 $\text{[math]}$ ，将0.00000201用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九下·北京市开学考) 下列图形中，是中心对称图形但不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022八下·上城期中) 如果一个多边形的内角和等于它的外角和的3倍，则这个多边形是（　　）

A . 三角形 B . 四边形 C . 六边形 D . 八边形

答案解析收藏纠错 + 选题
4. (2022九下·北京市开学考) 如图，下列选项中不能判定△ACD∽△ABC的是（　　）

A . ∠ACD＝∠B B . ∠ADC＝∠ACB C . AC²＝AD•AB D . BC²＝BD•AB

答案解析收藏纠错 + 选题
5. (2022九下·北京市开学考) 将函数 $\text{[math]}$ 的图象向左平移1个单位，再向上平移3个单位，可得到的抛物线是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九下·北京市开学考) 如图，圆是大正方形的内切圆，同时又是小正方形的外接圆，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部 $\text{[math]}$ 阴影 $\text{[math]}$ 区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九下·北京市开学考) 设m是非零实数，给出下列四个命题：①若-1<m<0，则 $\text{[math]}$ <m< $\text{[math]}$ ；②若m>1，则 $\text{[math]}$ < $\text{[math]}$ <m；③若m< $\text{[math]}$ < $\text{[math]}$ ，则m<0；④ $\text{[math]}$ <m< $\text{[math]}$ ，则0<m<1．其中命题成立的序号是（）

A . ①③ B . ①④ C . ②③ D . ③④

答案解析收藏纠错 + 选题
8. (2022九上·通州期中) 在特定条件下，篮球赛中进攻球员投球后，篮球的运行轨迹是开口向下的抛物线的一部分．“盖帽”是一种常见的防守手段，防守队员在篮球上升阶段将球拦截即为“盖帽”，而防守队员在篮球下降阶段将球拦截则属“违规”．对于某次投篮而言，如果忽略其他因素的影响，篮球处于上升阶段的水平距离越长，则被“盖帽”的可能性越大．收集几次篮球比赛的数据之后，某球员投篮可以简化为下述数学模型：如图所示，该球员的投篮出手点为P，篮框中心点为Q，他可以选择让篮球在运行途中经过A，B，C，D四个点中的某一点并命中Q，忽略其他因素的影响，那么被“盖帽”P的可能性最大的线路是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·坪山模拟) 分解因式： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
10. (2022九下·北京市开学考) 能说明命题“若a＞b，则ac＞bc”是假命题的一个c值是．

答案解析收藏纠错 + 选题
11. (2022九下·北京市开学考) 如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAC+∠ACD＝°．

答案解析收藏纠错 + 选题
12. (2022九下·北京市开学考) 如图，A(1，1)，B(2，2)，双曲线y= $\text{[math]}$ 与线段AB有公共点，则k的取值范围是。

答案解析收藏纠错 + 选题
13. (2022九下·北京市开学考) 关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则m的取值范围是．

答案解析收藏纠错 + 选题
14. (2022·门头沟模拟) 如图，半径为 $\text{[math]}$ 的⊙ $\text{[math]}$ 与边长为 $\text{[math]}$ 的等边三角形 $\text{[math]}$ 的两边 $\text{[math]}$ 、 $\text{[math]}$ 都相切，连接 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022九下·北京市开学考) 如图，△ABC的顶点A，B，C都在边长为1的正方形网格的格点上，BD⊥AC于点D，则AC的长为，BD的长为．

答案解析收藏纠错 + 选题
16. (2022九下·北京市开学考) 在平面直角坐标xOy中，已知点 $\text{[math]}$ ， ⊙P的半径为1，直线 $\text{[math]}$ ，给出以下四个结论：①当 $\text{[math]}$ 时，直线l与⊙P相离；②若直线l是⊙P的一条对称轴，则 $\text{[math]}$ ；③若直线l是⊙P只有一个公共点A，则 $\text{[math]}$ ；④若直线l上存在点B，⊙P上存在点N，使得 $\text{[math]}$ ，则a的最小值为 $\text{[math]}$ ，其中所有正确的结论序号是．

答案解析收藏纠错 + 选题

三、解答题

17. (2022九下·北京市开学考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022九下·北京市开学考) 解不等式组： $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2022九下·北京市开学考) 下面是小东设计的“作圆的一个内接矩形，并使其对角线的夹角为60°”的尺规作图过程．
已知：⊙O
求作：矩形ABCD，使得矩形ABCD内接于⊙O，且其对角线AC，BD的夹角为60°．
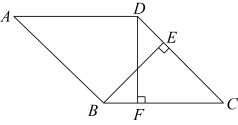
作法：如图
①作⊙O的直径AC；
②以点A为圆心，AO长为半径画弧，交直线AC上方的圆弧于点B；
③连接BO并延长交⊙O于点D；
所以四边形ABCD就是所求作的矩形．
根据小东设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  证明：∵点A，C都在⊙O上，
  ∴OA＝OC
  同理OB＝OD
  ∴四边形ABCD是平行四边形
  ∵AC是⊙O的直径，
  ∴∠ABC＝90°（）（填推理的依据）
  ∴四边形ABCD是矩形
  ∵AB＝ ▲ ＝BO，
  ∴四边形ABCD四所求作的矩形．
答案解析收藏纠错 + 选题
20. (2022九下·北京市开学考) 若 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
21. (2022九下·北京市开学考) 如图，在菱形ABCD中，BE⊥CD于点E．DF⊥BC于点F．
1. （1）求证：BF＝DE；
2. （2）分别延长BE和AD交于点G，若 $\text{[math]}$ ，求DG的值．
答案解析收藏纠错 + 选题
22. (2022九下·北京市开学考) 今年通州区在老旧小区改造方面取得了巨大成就，人居环境得到了很大改善．如图，某小区规划在长16m，宽9m的矩形场地ABCD上，修建同样宽的小路，使其中的小路分别与AB和AD平行，其余部分种草．通过测量可知草坪的总面积为112m² ，求小路的宽．

答案解析收藏纠错 + 选题
23. (2022九下·北京市开学考) 在平面直角坐标系xOy中，函数y= $\text{[math]}$ （x＞0）的图象与直线y=mx交于点A（2，2）．
1. （1）求k，m的值；
2. （2）点P的横坐标为n（n＞0），且在直线y=mx上，过点P作平行于x轴的直线，交y轴于点M，交函数y= $\text{[math]}$ （x＞0）的图象于点N．
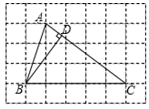
  ①n=1时，用等式表示线段PM与PN的数量关系，并说明理由；
  ②若PN≥3PM，结合函数的图象，直接写出n的取值范围．
答案解析收藏纠错 + 选题
24. (2022九下·北京市开学考) 如图，AB是⊙O的直径，点D，E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
1. （1）求证：CE是⊙O的切线；
2. （2）若⊙O的半径长为5，BF=2，求EF的长．
答案解析收藏纠错 + 选题
25. (2022九下·北京市开学考) 为了研究一种新药的疗效，选100名患者随机分成两组，每组各50名，一组服药，另一组不服药，12周后，记录了两组患者的生理指标 $\text{[math]}$ 和 $\text{[math]}$ 的数据，并制成下图，其中“*”表示服药者，“+”表示未服药者；

同时记录了服药患者在4周、8周、12周后的指标z的改善情况，并绘制成条形统计图．

根据以上信息，回答下列问题：
1. （1）从服药的50名患者中随机选出一人，求此人指标 $\text{[math]}$ 的值大于1.7的概率；
2. （2）设这100名患者中服药者指标 $\text{[math]}$ 数据的方差为 $\text{[math]}$ ，未服药者指标 $\text{[math]}$ 数据的方差为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ；（填“>”、“=”或“<” ）
3. （3）对于指标z的改善情况，下列推断合理的是．
  ①服药4周后，超过一半的患者指标z没有改善，说明此药对指标z没有太大作用；
  
  ②在服药的12周内，随着服药时间的增长，对指标z的改善效果越来越明显．
答案解析收藏纠错 + 选题
26. (2022九下·北京市开学考) 已知，在平面直角坐标系xOy中，二次函数的解析式为 $\text{[math]}$ ．
1. （1）对于任意的常数a，二次函数是否经过定点，若经过，请求出此定点？若不经过，请说明理由；
2. （2）当x≥a时，二次函数的图象记为图象G．
  ①当图象G与坐标轴有两个不同交点时，求a的取值范围；
  ②当图象G上恰有3个点到x轴的距离为1时，请直接写出a的取值范围．
答案解析收藏纠错 + 选题
27. (2022九下·北京市开学考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， D为BC延长线上一点，点E为线段AC，CD的垂直平分线的交点，连接EA，EC，ED．
1. （1）如图1，当 $\text{[math]}$ 时，则 $\text{[math]}$ °；
2. （2）当 $\text{[math]}$ 时，
  ①如图2，连接AD，判断 $\text{[math]}$ 的形状，并证明；
  ②如图3，直线CF与ED交于点F，满足 $\text{[math]}$ ． P为直线CF上一动点．当 $\text{[math]}$ 的值最大时，用等式表示PE，PD与AB之间的数量关系为 ▲ ，并证明．
答案解析收藏纠错 + 选题
28. (2022九下·北京市开学考) 在平面直角坐标系xOy中，点A(a，b)和点B(c，d)．给出如下定义：以AB为边，作等边三角形ABC，按照逆时针方向排列A，B，C三个顶点，则称等边三角形ABC为点A，B的逆序等边三角形．例如，当 $\text{[math]}$ 时，点A，B的逆序等边三角形ABC如图①所示．
1. （1）已知点A(-1，0)，B(3，0)，则点C的坐标为；请在图①中画出点C，B的逆序等边三角形CBD，点D的坐标为．
2. （2）图②中，点B(3，0)，点A在以点M(-2，0)为圆心1为半径的圆上，求点A，B的逆序等边三角形ABC的顶点C的横坐标取值范围．
3. （3）图③中，点A在以点M(-2，0)为圆心1为半径的圆上，点B在以N(3，0)为圆心2为半径的圆上，且点B的纵坐标 $\text{[math]}$ ，点A，B的逆序等边三角形ABC如图③所示．若点C恰好落在直线 $\text{[math]}$ 上，直接写出t的取值范围．
答案解析收藏纠错 + 选题