
|
编号 |
1 |
2 |
3 |
4 |
5 |
6 |
|
质量(克) |
126 |
127 |
124 |
126 |
123 |
125 |
|
差值(克) |
+1 |
,其中
,
.
② ;
③ .
a.确定和的绝对值: ;
b.确定和的符号:计算出加数+2和-3的绝对值,分别是2和3,通过比较它们的绝对值发现,加数-3的绝对值较大,写出和的符号为“-”;
c.写出计算结果;
d.决定应用有理数加法法则中“异号的两个数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值”;
e.判断出是两个有理数相加的问题;
f.观察两个加数的符号,发现是异号两数相加.
小明同学不小心把顺序写乱了,请你仔细阅读他的思考过程,写出正确的顺序;
![]()
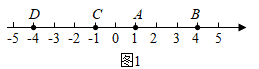
小明在学习过程中,发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示,如图1所示,线段 ,
,
的长度可表示为:
;
BC=5=4-(-1);
;
于是他归纳出这样的结论:如果点 表示的数为
,点
表示的数为
,当
时,
(较大数-较小数).

①如图2所示,计算: ,
;
②把一条数轴在数 处对折,使表示-20和2020两数的点恰好互相重合,则
=;
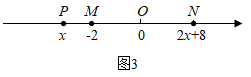
①如图3所示,点 表示数
,点
表示数-2,点
表示数
,且
,求出点
和点
分别表示的数;
②在上述①的条件下,是否存在点 ,使
?若存在,求出点
所表示的数;若不存在,请说明理由.