一、选择题(本大题共10小题,每小题4分,共40分・请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
-
-
A . 0<y1<y2
B . 0<y2<y1
C . y1<y2<0
D . y2<y1<0
-
4.
(2021九上·临海期末)
袋中装有4个红球,2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下, 一次性随机地从袋子中摸出三个球,则下列事件发生的概率最大的是( )
A . 有两个黄球
B . 三个都是黄球
C . 三个都是红球
D . 至少一个红球
-
5.
(2021九上·临海期末)
某地政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品经过两次降价后, 由每盒64元下调至36元,若设每次平均降价的百分率为x,由题意可列方程为( )
A . 64(1-x)2=36
B . 36(1+x)2=64
C . 64 (1-2x)=36
D . 36(1+2x)=64
-
6.
(2021九上·临海期末)
如图,AB为⊙O直径,按如下步骤作图:①以点A为圆心,适当的长为半径做圆弧交⊙O于点C,D;②连接AC,AD,BC,BD.则下列结论不一定成立的是( )
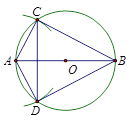
A . AB⊥CD
B . BC=BD
C . ∠CBD =2∠ACD
D . BC=CD
-
7.
(2021九上·临海期末)
向下图所示的空水壶内匀速注水,则下列描述壶内水的深度h (单位:cm)与注水时间t (单位:秒)关系的函数图象中,正确的是( )

-
A . 沿一条对角线所在直线翻折,两旁的部分能互相重合
B . 沿一条边的垂直平分线翻折,两旁的部分能互相重
C . 绕对角线交点旋转90°,能与自身重合
D . 绕对角线交点旋转180°,能与自身重合
-
9.
(2021九上·临海期末)
一元二次方程ax
2+bx+c=0有两个不相等的实数根m, n ,点A(x
1 , y
1),B(x
2 , y
2)在二次函数y=ax
2+bx+c的图象上,则下列条件一定能判断y
1= y
2的是( )
A . x1=m+2, x2= n +2
B . x1=m-2, x2= n -2
C . x1=m+2,x2= n -2
D . x1=2m, x2= 2n
-
10.
(2021九上·临海期末)
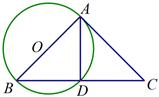
如图,点C在直径为AB的半圆上,∠ABC=30°,AB=4,分别以AC,BC为直径作半圆,均与AB交于点D,则阴影部分的面积为( )

A . π+2  B . 2π+4
C . 4π-8
D . 4π-4
B . 2π+4
C . 4π-8
D . 4π-4 
二、填空题(本大题共6小题,每小题5分,共30分)
-
11.
(2021九上·临海期末)
某林业部门要考察某种幼树在一定条件下的移植成活率,在同样的条件下对这种幼树进行大量移植,并统计成活情况,记录如下:
|
移植总数(n)
|
50
|
200
|
1000
|
5000
|
10000
|
|
成活(m)
|
46
|
171
|
912
|
4480
|
9020
|
|
成活的频率(  ) )
|
0.920
|
0.855
|
0.912
|
0.896
|
0.902
|
由此可以估计幼树移植成活的概率为(结果保留小数点后一位)
-
12.
(2021九上·临海期末)
若正比例函数y=mx和反比例函数y=

的图象交于点A,B,点A的坐标为(2 ,4),则点B的坐标为
.
-
13.
(2021九上·临海期末)
如图,圆锥形反光路锥在夜间能起到很好的警示作用,若圆锥的底面半径为10cm,母线长为50cm,则圆的侧面积为
cm
2

-
14.
(2021九上·临海期末)
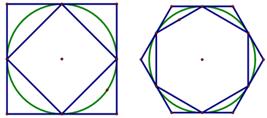
我国古代数学家刘徽创造的“割圆术”,利用了圆内接正多边形和外切正多边形的面积或周长,无限逼近圆来近似估计圆的面积或周长,从而估算出π的范围.如图1,用圆内接正方形和外切正方形周长可得2

<r<4,那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到
(结果保留根号)
-
15.
(2021九上·临海期末)
二次函数y=ax
2+bx+c的图象与y轴交于点(0,-3),与x轴两个交点的横坐标分别为m,n,则a(m
2+n
2)+b(m+n)的值为
-
16.
(2021九上·临海期末)
如图,点P在正方形ABCD的对角线AC上,PE⊥PB于点P,交AD于点E,若△PAE的面积占正方形ABCD面积的

,则

=

三、解答题(本题有8小题,第17 20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分
-
-
18.
(2021九上·临海期末)
为弘扬中华优秀传统文化,某校组织《诗词大会》比赛,其中一个环节的题目涵盖“豪放”“婉约”“咏物”“咏怀”四大类(分别写在4张卡片上),由一位比赛选手随机抽取一张卡片,记下题目类别后,放回洗均匀后由下一位选手抽取。
-
-
(2)
用画树状图或列表的方法求乙,丙两选手抽到同类别题目的概率。
-
19.
(2021九上·临海期末)
一辆汽车前灯电路上的电压U保持不变,通过调节车灯的电阻值可以改变灯的亮度,下表记录了电流I随电阻R的变化情况:
|
R/Ω
|
…
|
2
|
3
|
4
|
5
|
6
|
…
|
|
I/A
|
…
|
6
|
4
|
3
|
2.4
|
2
|
…
|
-
-
(2)
若车灯通过的最大电流为10A,则车灯电阻的阻值至少是多少?
-
-
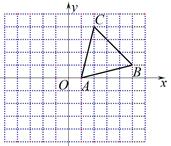
(1)
请画出△ABC绕点A逆时针旋转90°所得的△AB1C1 , 并写出点C1的坐标;
-
(2)
在(1)的条件下,直接写出△BB1C1的外接圆圆心的坐标.
-
-
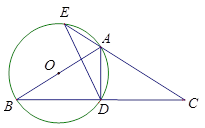
(1)
如图1,若BC=2AD,求证: AC是⊙O的切线;
-
(2)
如图2,若CA的延长线交⊙O于点E,DE

AD=1,AB=5,求△ABC的面积.
-
-
-
(2)
若将该抛物线向右平移6个单位,求平移所得抛物线与原抛物线的交点坐标;
-
(3)
将抛物线y=a(x-2)2沿射线BA方向平移,在平移过程中抛物线能否经过原点? 请说明理由.
-
23.
(2021九上·临海期末)
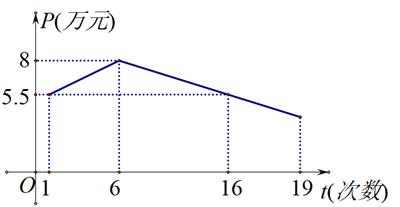
王大伯有一条渔船用于捕鱼和捕蟹作业,一年共安排20次出海作业,其中x次捕鱼,t次捕蟹 (x,t均为正整数,且x+t=20).每次捕鱼的平均收入y(单位:万元)与捕鱼次数x的关系为

,每次捕蟹的平均收入p(单位:万元)与捕蟹次数t的关系如图所示.
-
-
(2)
设王大伯捕鱼和捕蟹的年总收入为W(单位:万元)
①若x=8,W的值为;
②求W关于x的函数解析式.
-
(3)
王大伯一年的收入能否超过216万元? 若能,请写出如何安排捕鱼和捕蟹次数;若不能,请说明理由.
-
24.
(2021九上·临海期末)
如图,AB是⊙O的直径,点D,E在⊙O上,∠AOD=∠BOE=45°,点C在

上运动,OD,OE分别交AC,BC于点M,N,连接MN.

-
-
(2)
若AB=6
①判断 DM+EN的长是否为定值?若是,请求出该定值;若不是,请说明理由;
②若四边形MABN的面积为6.5,求MN的长.
-
(3)
设AB=a,MN=b,则四边形MABN的面积为(用含a,b的代数式表示)
 B .
B .  C .
C .  D .
D . 


 B .
B . 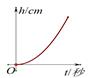 C .
C .  D .
D .