 B .
B .  C .
C .  D .
D . 
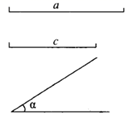
求作: ,使
,
,(用尺规作图,保留作图痕迹,不写作法).
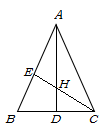
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的
是唯一的,依据是三角形全等判定定理中的_▲_.
( 1 )A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个;
( 2 )E类为自拟其它与疫情相关的主题.
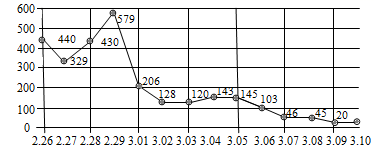
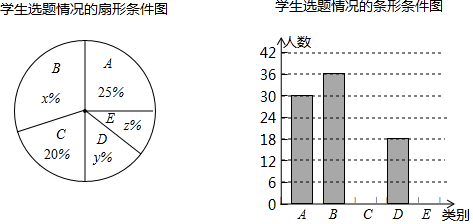
评奖之余,为了解学生的选题倾向,发掘出最能引发学生触动的主题素材,组织者随机抽取了部分作品进行了统计,并将统计结果绘制成了如下两幅尚不完整的统计图.
请根据以上信息回答:
①求 的面积;
②点 是一动点,若三角形
的面积等于三角形
的面积.请直接写出点
坐标.
|
物资种类 |
食品 |
药品 |
生活用品 |
|
每辆汽车运载量/吨 |
6 |
5 |
4 |
|
每吨所需运费/元 |
120 |
160 |
100 |
①求证: 是“近直角三角形”;
②求 的长.