 B .
B .  C .
C .  D .
D . 




甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 .(在横线上填写正确的序号)


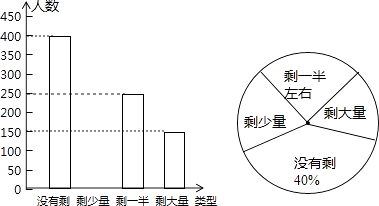
游戏规则:随机转动转盘两次,停止后,指针各指向一个数字,若两数之积为偶数,则小明胜;否则小华胜.
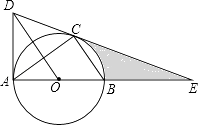
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).

①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.

线段AD与BE所成的锐角度数为°;
灵活运用:
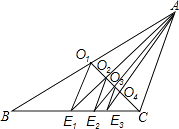
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.

