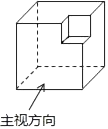
 B .
B .  C .
C .  D .
D . 
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )




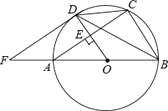
如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.
(参考数据:sin22°≈ ,cos22°≈
,tan22°≈
)





如图1,抛物线y=ax2+bx+4的图象过A(﹣1,0),B(4,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.

①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接CF,将△PCF沿CF折叠得到△P′CF,当t为何值时,四边形PFP′C是菱形?