



应试者 | 测试成绩 | ||
创新能力 | 计算机能力 | 公关能力 | |
甲 | 72 | 50 | 88 |
乙 | 85 | 74 | 45 |
如果公司赋予“创新能力”、“计算机能力”、“公关能力”三项的权重为5:3:2,则本次招聘中应试者将被录用(填“甲”或“乙”)

(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)



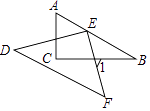
①作△ABC的外接圆O;
②在AB的延长线上作一点D,使得CD与⊙O相切;
折纸三等分角 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角. 如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法: ①在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图1; ②翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图2; ③折出射线BQ,BT,得到图3,则射线BQ,BT就是∠SBC的三等分线.
下面是证明BQ,BT是∠SBC三等分线的部分过程: 证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形 根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB ∴△EBT≌△QTB, ∴∠BQT=∠TEB=90°, ∴BQ⊥PT … |
学习任务:
信息1:2015年的绿地总面积(绿地总面积=森林面积+草场面积)为276km2 , 其中森林面积比上一年增长40%,草地面积比上一年增长20%.
信息2:2014年的绿地总面积为200km2 .

求:
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
问题情境:
如图(1),在△ABC中,∠ACB=90°,AC=BC=a,点D为AB上一点(0<AD< AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.

解决问题:
下面是学习小组提出的三个问题,请你解答这些问题:

提出问题:
“智慧”小组提出的问题是:当AD为何值时,四边形DGFH的面积最大?
请你参照智慧小组的做法,再提出一个与四边形DGFH有关的数学问题(提出问题即可,不要求进行解答,但所提问题必须有效)
你提出的问题是:

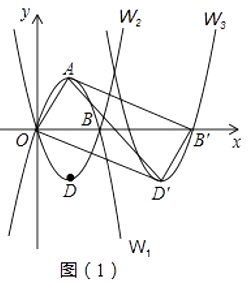
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
