
参考数据: ,
| | | | | | |
| 275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中 ,
附:对于一组数据 ,
,
,其回归直线
的斜率和截距的最小二乘估计分别为
,
.
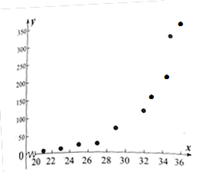
①试求 关于
回归方程;
②已知用人工培养该昆虫的成本 与温度
和产卵数
的关系为
,当温度
(
取整数)为何值时,培养成本的预报值最小?
(I)根据所抽取的样本数据,填写答题卷中的列联表. 并根据 统计量判断能否有
的把握认为选择物理还是历史与性别有关?
(II)在样本里选历史的人中任选4人,记选出4人中男生有 人,女生有
人,求随机变量
的分布列和数学期望.(
的计算公式见下)
,临界值表:
| | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |