黑龙江省哈尔滨市师大附中2019-2020学年高二下学期理数...

更新时间：2021-04-22 浏览次数：94 类型：期中考试

一、单选题

1. (2020高二下·哈尔滨期中) 甲乙和其他2名同学合影留念，站成两排两列，且甲乙两人不在同一排也不在同一列，则这4名同学的站队方法有（）

A . 8种 B . 16种 C . 32种 D . 64种

答案解析收藏纠错 + 选题
2. (2020高二下·哈尔滨期中) 函数 $\text{[math]}$ 在 $\text{[math]}$ 上取最大值时， $\text{[math]}$ 的值为（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020高二下·哈尔滨期中) 某班共有学生52人，现根据座号，用系统抽样的方法，抽取一个容量为4的样本．已知5号、18号、44号同学在样本中，那么样本中还有一个同学的座号是（）

A . 23 B . 27 C . 31 D . 33

答案解析收藏纠错 + 选题
4. (2021高一下·陈仓期末)
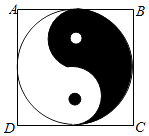
如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020高二下·哈尔滨期中) 在 $\text{[math]}$ 的展开式中，含 $\text{[math]}$ 项的系数为（）

A . 16 B . -16 C . 8 D . -8

答案解析收藏纠错 + 选题
6. (2022高二下·石景山期末) 从 $\text{[math]}$ 中任取2个不同的数，事件 $\text{[math]}$ “取到的2个数之和为偶数”，事件 $\text{[math]}$ “取到两个数均为偶数”，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020高二下·哈尔滨期中) 已知a为函数f（x）=x³–12x的极小值点，则a=（）

A . –4 B . –2 C . 4 D . 2

答案解析收藏纠错 + 选题
8. (2020高二下·哈尔滨期中) 某班某天上午有五节课，需安排的科目有语文，数学，英语，物理，化学，其中语文和英语必须连续安排，数学和物理不得连续安排，则不同的排课方法数为（）

A . 60 B . 48 C . 36 D . 24

答案解析收藏纠错 + 选题
9. (2020高二下·哈尔滨期中) 函数 $\text{[math]}$ 的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2020高二下·辽宁期中) 某学习小组有三名男生、三名女生共计六名同学，选出四人进行学业水平测试，这四人中所含女生人数记为 $\text{[math]}$ ，则 $\text{[math]}$ 的数学期望为（）

A . 1 B . $\text{[math]}$ C . 2 D . 3

答案解析收藏纠错 + 选题
11. (2020高二下·哈尔滨期中) 已知A，B分别是双曲线 $\text{[math]}$ 的左右顶点，点M在E上.且 $\text{[math]}$ ，则双曲线E的渐近线方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2020高二下·哈尔滨期中) 已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ ， $\text{[math]}$ 为其导函数，满足 $\text{[math]}$ ，且 $\text{[math]}$ ，若不等式 $\text{[math]}$ 对任意 $\text{[math]}$ 恒成立，则实数a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2020高二下·淮安期末) 曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程为.

答案解析收藏纠错 + 选题
14. (2021高二下·乌海期末) 一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X表示抽到的二等品件数，则DX=．

答案解析收藏纠错 + 选题
15. (2020高二下·哈尔滨期中) 如图，圆形纸片的圆心为 $\text{[math]}$ ，半径为 $\text{[math]}$ ，该纸片上的等边三角形 $\text{[math]}$ 的中心为 $\text{[math]}$ . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为圆 $\text{[math]}$ 上的点， $\text{[math]}$ 分别是以 $\text{[math]}$ 为底边的等腰三角形.沿虚线剪开后，分别以 $\text{[math]}$ 为折痕折起 $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 重合，得到三棱锥.当所得三棱锥体积（单位： $\text{[math]}$ ）最大时， $\text{[math]}$ 的边长为（ $\text{[math]}$ ）.

答案解析收藏纠错 + 选题
16. (2020高二下·哈尔滨期中) 若 $\text{[math]}$ ，则（1） $\text{[math]}$ ；（2） $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

17. (2020高二下·哈尔滨期中) 已知函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的单调区间；
2. （2）当 $\text{[math]}$ ，且 $\text{[math]}$ 时，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2020高二下·辽宁期中) 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ，η，已知甲、乙两名射手在每次射击中射中的环数大于6环，且甲射中10，9，8，7环的概率分别为0.5，3a，a，0.1，乙射中10，9，8环的概率分别为0.3，0.3，0.2.
1. （1）求ξ，η的分布列；
2. （2）求ξ，η的数学期望与方差，并以此比较甲、乙的射击技术．
答案解析收藏纠错 + 选题
19. (2020高二下·辽宁期中) 已知函数 $\text{[math]}$ ，函数图象上有两动点 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）用 $\text{[math]}$ 表示在点 $\text{[math]}$ 处的切线方程；
2. （2）若动直线 $\text{[math]}$ 在 $\text{[math]}$ 轴上的截距恒等于 $\text{[math]}$ ，函数在 $\text{[math]}$ 、 $\text{[math]}$ 两点处的切线交于点 $\text{[math]}$ ，求证：点 $\text{[math]}$ 的纵坐标为定值.
答案解析收藏纠错 + 选题
20. (2020高二下·哈尔滨期中) 国庆70周年阅兵式上的女兵们是一道靓丽的风景线，每一名女兵都是经过层层筛选才最终入选受阅方队，筛选标准非常严格，例如要求女兵身高（单位：cm）在区间 $\text{[math]}$ 内.现从全体受阅女兵中随机抽取200人，对她们的身高进行统计，将所得数据分为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五组，得到如图所示的频率分布直方图，其中第三组的频数为75，最后三组的频率之和为0.7.

参考数据：若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）请根据频率分布直方图估计样本的平均数 $\text{[math]}$ 和方差 $\text{[math]}$ （同一组中的数据用该组区间的中点值代表）；
2. （2）根据样本数据，可认为受阅女兵的身高X（cm）近似服从正态分布 $\text{[math]}$ ，其中 $\text{[math]}$ 近似为样本平均数 $\text{[math]}$ ， $\text{[math]}$ 近似为样本方差 $\text{[math]}$ .
  （i）求 $\text{[math]}$ ；
  
  （ii）若从全体受阅女兵中随机抽取10人，求这10人中至少有1人的身高在174.28cm以上的概率.
答案解析收藏纠错 + 选题
21. (2020高二下·哈尔滨期中) 2018年3月份，上海出台了《关于建立完善本市生活垃圾全程分类体系的实施方案》，4月份又出台了《上海市生活垃圾全程分类体系建设行动计划（2018-2020年）》，提出到2020年底，基本实现单位生活垃圾强制分类全覆盖，居民区普遍推行生活垃圾分类制度．为加强社区居民的垃圾分类意识，推动社区垃圾分类正确投放，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需要征集一部分垃圾分类志愿者．
1. （1）为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关，现随机选取了一部分社区居民进行调查，其中被调查的男性居民和女性居民人数相同，男性居民中不喜欢担任垃圾分类志愿者占男性居民的 $\text{[math]}$ ，女性居民中不喜欢担任垃圾分类志愿者占女性居民的 $\text{[math]}$ ，若研究得到在犯错误概率不超过0.010的前提下，认为居民喜欢担任垃圾分类志愿者与性别有关，则被调查的女性居民至少多少人？
  附 $\text{[math]}$ ， $\text{[math]}$ ，
  
  $\text{[math]}$
  
  0.100
  
  0.050
  
  0.010
  
  0.005
  
  0.001
  
  $\text{[math]}$
  
  2.706
  
  3.841
  
  6.635
  
  7.879
  
  10.828
2. （2）某垃圾站的日垃圾分拣量 $\text{[math]}$ （千克）与垃圾分类志愿者人数 $\text{[math]}$ （人）满足回归直线方程 $\text{[math]}$ ，数据统计如下：
  
  志愿者人数 $\text{[math]}$ （人）
  
  2
  
  3
  
  4
  
  5
  
  6
  
  日垃圾分拣量 $\text{[math]}$ （千克）
  
  25
  
  30
  
  40
  
  45
  
  $\text{[math]}$
  
  已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，根据所给数据求 $\text{[math]}$ 和回归直线方程 $\text{[math]}$ ，附： $\text{[math]}$ ， $\text{[math]}$ ．
3. （3）用（2）中所求的线性回归方程得到与 $\text{[math]}$ 对应的日垃圾分拣量的估计值 $\text{[math]}$ ．当分拣数据 $\text{[math]}$ 与估计值 $\text{[math]}$ 满足 $\text{[math]}$ 时，则将分拣数据 $\text{[math]}$ 称为一个“正常数据”．现从5个分拣数据中任取3个，记 $\text{[math]}$ 表示取得“正常数据”的个数，求 $\text{[math]}$ 的分布列和数学期望．
答案解析收藏纠错 + 选题
22. (2020高二下·哈尔滨期中) 已知函数 $\text{[math]}$ ，其中e为自然对数的底数.
1. （1）若曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线为 $\text{[math]}$ ，求a的值；
2. （2）若函数 $\text{[math]}$ 的极小值为 $\text{[math]}$ ，求a的值；
3. （3）若 $\text{[math]}$ ，证明：当 $\text{[math]}$ 时， $\text{[math]}$ .
答案解析收藏纠错 + 选题