

 B .
B . 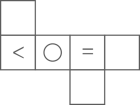 C .
C .  D .
D . 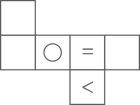
![]()

如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.

解:因为∠AOC=2∠BOC,∠BOC=40°,
所以∠AOC= ▲ °,
所以∠AOB=∠AOC+∠ ▲ =120°.
因为OD平分∠AOB,
所以∠AOD= ∠ ▲ = ▲ °,
所以∠COD=∠ ▲ ﹣∠AOD= ▲ °.

|
星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
|
与计划量的差值 |
| | | | | | |
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:

求(2)中式子的值.
问题情境
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动,发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点C是线段AB上的一点,M是AC的中点,N是BC的中点.
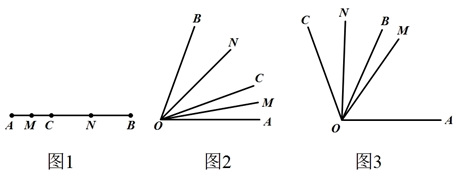
①若AB=6,AC=2,求MN的长度.(写出计算过程)
②若AB=a , AC=b , 则MN= ▲ . (直接写出结果)
“创新”小组的同学类比想到:如图2,已知∠AOB=70°,在角的内部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON .
③若∠AOC=20°,求∠MON的度数.(写出计算过程)
④若∠AOC=m , 则∠MON= ▲ . (直接写出结果)
“慎密”小组在“创新”小组的基础上提出:如图3,若∠AOB=n , 在角的外部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON , 若∠AOC=m , 则∠MON=.(直接写出结果)