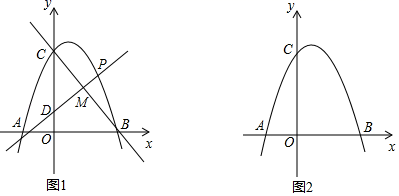B .
B . 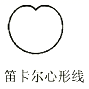 C .
C .  D .
D . 
①平均数是5,②中位数是4,③众数是4,④方差是4.4,其中正确的个数为( )
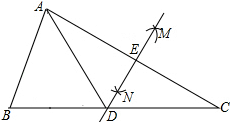

 B .
B .  C .
C .  D .
D . 
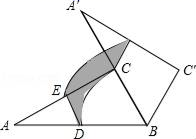

|
年级 |
七年级 |
八年级 |
|
平均数 |
92 |
92 |
|
中位数 |
93 |
b |
|
众数 |
c |
100 |
|
方差 |
52 |
50.4 |

根据以上信息,解答下列问题:
| 销售单价 | 14 | 18 | 22 | 26 |
| 日销售量 | 240 | 180 | 120 | |
(注:日销售利润=日销售量×(销售单价-成本单价))
① 元;
②当销售价格 元时,日销售利润
最大,最大值是元;

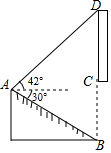
如图①,若点D在BC的延长线上,试猜想AP,CD,BC之间的数量关系为;
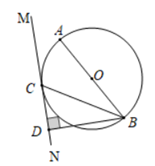
如图②,若点D在线段BC上,试猜想AP,CD,BC之间的数量关系,并说明理由;
当E为BP的中点时,直接写出线段CD的长度.