河北省唐山市古冶区2019-2020学年八年级下学期数学期末...

更新时间：2021-05-19 浏览次数：263 类型：期末考试

一、单选题

1. (2020八下·古冶期末) 下列图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八下·古冶期末) 下列运算错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020八下·古冶期末) 下列二次根式是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020八下·古冶期末) 平行四边形的一个内角为 $\text{[math]}$ ，与它相邻的另一个内角等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020八下·古冶期末) 甲和乙一起练习射击，第一轮10枪打完后两人的成绩如图所示．设他们这10次射击成绩的方差为 $\text{[math]}$ 、 $\text{[math]}$ ，下列关系正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
6. (2020八下·古冶期末) 已知点 $\text{[math]}$ 和点 $\text{[math]}$ 是正比例函数 $\text{[math]}$ 图象上的两点，则a与b的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 以上都不对

答案解析收藏纠错 + 选题
7. (2020八下·古冶期末) 某公司10名职工的5月份工资统计如下，该公司10名职工5月份工资的众数和中位数分别是（）

工资（元）

2000

2200

2400

2600

人数（人）

1

3

4

2

A . 2400元、2400元 B . 2400元、2300元 C . 2200元、2200元 D . 2200元、2300元

答案解析收藏纠错 + 选题
8. (2020八下·古冶期末) 已知在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ，点B在直线 $\text{[math]}$ 上，则 $\text{[math]}$ 两点间的最小距离是（）

A . 1 B . $\text{[math]}$ C . 2 D . 4

答案解析收藏纠错 + 选题
9. (2020八下·古冶期末) 现有两根铁棒，它们的长分别为2米和3米，如果想焊接一个直角三角形铁架，那么第三根铁棒的长为（）

A . $\text{[math]}$ 米 B . 5米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米或 $\text{[math]}$ 米

答案解析收藏纠错 + 选题
10. (2020八下·古冶期末) 菱形ABCD的对角线AC=6，BD=8，那么边AB的长度是（）

A . 10 B . 5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2020八下·古冶期末) 如图，在△ABC中，D、E分别是AB、AC的中点，AC=8，F是DE上一点，连接AF，CF，DF=1，若∠AFC=90°，则BC的长度为（）

A . 10 B . 12 C . 14 D . 16

答案解析收藏纠错 + 选题
12. (2020八下·古冶期末) 甲乙两城市相距600千米，一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市．已知货车出发1小时后客车再出发，先到终点的车辆原地休息．在汽车行驶过程中，设两车之间的距离为s（千米），客车出发的时间为t（小时），它们之间的关系如图所示，则下列结论错误的是（）

A . 货车的速度是60千米/小时 B . 离开出发地后，两车第一次相遇时，距离出发地150千米 C . 货车从出发地到终点共用时7小时 D . 客车到达终点时，两车相距180千米

答案解析收藏纠错 + 选题

二、填空题

13. (2024八下·昭阳月考) 化简 $\text{[math]}$ =

答案解析收藏纠错 + 选题
14. (2020八下·古冶期末) 若直角三角形的两直角边的长分别为a、b，且满足 $\text{[math]}$ ，则该直角三角形的斜边长为．

答案解析收藏纠错 + 选题
15. (2022八下·道里期末) 将一次函数 $\text{[math]}$ 的图象向上平移3个单位，所得的直线不经过第象限．

答案解析收藏纠错 + 选题
16. (2020八下·古冶期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ 后得到 $\text{[math]}$ （点B的对应点是 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点是 $\text{[math]}$ ），连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021八下·巢湖期末) 甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选同学．

甲

乙

丙

丁

平均数

80

85

85

80

方差

42

42

54

59

答案解析收藏纠错 + 选题
18. (2020八下·古冶期末) 在数学课上，老师提出问题：如图，将锐角三角形纸片 $\text{[math]}$ 经过两次折叠，得到边 $\text{[math]}$ 上的点 $\text{[math]}$ ，使得四边形 $\text{[math]}$ 恰好为菱形．小明给出的折叠方法：如图，① $\text{[math]}$ 边向 $\text{[math]}$ 边折叠，使 $\text{[math]}$ 边落在 $\text{[math]}$ 边上，得到折痕交 $\text{[math]}$ 于D；②C点向 $\text{[math]}$ 边折叠，使C点与D点重合，得到折痕交 $\text{[math]}$ 边于E，交 $\text{[math]}$ 边于F．老师说：“小明的作法正确．”请回答：小明这样折叠的依据是①是平行四边形；②是菱形．

答案解析收藏纠错 + 选题

三、解答题

19. (2020八下·古冶期末) 如图，每个小方格都是边长为1的正方形．
1. （1）可得 $\text{[math]}$ 是直角三角形，请你说明理由：
2. （2） $\text{[math]}$ 的周长为，面积为．
答案解析收藏纠错 + 选题
20. (2020八下·古冶期末) 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系， $\text{[math]}$ 的顶点都在格点上，

⑴将 $\text{[math]}$ 绕点O顺时针旋转 $\text{[math]}$ 得到的 $\text{[math]}$ ，写出点 $\text{[math]}$ 和 $\text{[math]}$ 的坐标；

⑵将 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ 得到的 $\text{[math]}$ ，写出点 $\text{[math]}$ 和 $\text{[math]}$ 的坐标；

⑶已知 $\text{[math]}$ 关于直线l对称的 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，请直接写出直线l的函数解析式．

答案解析收藏纠错 + 选题

21. (2020八下·古冶期末) 李伯种植了100棵樱桃树，为了估计今年樱桃的收入情况，到收获时，从中随机选取了20棵树的樱桃采摘，并将采摘的情况绘制了条形统计图如下，请你根据这幅统计图中给出的信息回答下面的问题：

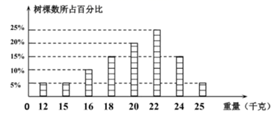
樱桃重量（千克/每棵）	12	15	16	18	20	22	24	25
树的棵数	1	1	2	3			3	1

（1）这20棵樱桃树所摘樱桃的平均重量为千克；
（2）这20棵樱桃树所摘樱桃重量的中位数是千克，众数是千克；
（3）请在以上平均数、中位数、众数三个数中，选择一个能更好地反映一棵樱桃树所摘樱桃重量平均水平的量，当每千克樱桃的批发价为12元，请估计李伯今年樱桃销售的总收入为多少元？

答案解析收藏纠错 + 选题

22. (2020八下·古冶期末) 如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，分别过点A，C作AE∥DC，CE∥AB，两线交于点E．
1. （1）求证：四边形AECD是菱形；
2. （2）如果∠B=60°，BC=2，求四边形AECD的面积．
答案解析收藏纠错 + 选题
23. (2020八上·德保期中) 在一段时间，某地区一种食品的需求量 $\text{[math]}$ （万斤）、供应量 $\text{[math]}$ （万斤）与价格x（元/斤）分别近似满足下列函数关系式： $\text{[math]}$ ， $\text{[math]}$ ．当需求量为0时，即停止供应．当 $\text{[math]}$ 时，该食品的价格称为稳定价格，需求量称为稳定需求量．
1. （1）求该食品的稳定价格与稳定需求量；
2. （2）当价格x在范围时，该商品的需求量低于供应量；
3. （3）当供应量低于需求量时，政府常通过对供应方提供价格补贴来提高供货量．当供应量降低到20万斤时，为使该食品达到稳定价格，政府每斤应补贴多少元？
答案解析收藏纠错 + 选题
24. (2020八下·古冶期末) 如图，在平面直角坐标系中，点O是坐标原点，四边形 $\text{[math]}$ 是菱形，点A的坐标为 $\text{[math]}$ ，点C在x轴的正半轴上，直线 $\text{[math]}$ 交y轴于点M， $\text{[math]}$ 边交y轴于点H，连接 $\text{[math]}$ ．
1. （1）菱形 $\text{[math]}$ 的边长是；
2. （2）求直线 $\text{[math]}$ 的解析式；
3. （3）动点P从点A出发，沿折线 $\text{[math]}$ 方向以2个单位/秒的速度向终点C匀速运动，设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，点P的运动时间为t秒，当点P在 $\text{[math]}$ 边上运动时，求S与t间的函数关系式．
答案解析收藏纠错 + 选题
25. (2020八下·古冶期末) 如图，已知 $\text{[math]}$ 是等腰直角三角形， $\text{[math]}$ ，点D是 $\text{[math]}$ 的中点．作正方形 $\text{[math]}$ ，使点A、C分别在边 $\text{[math]}$ 和 $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）猜想线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系是；
2. （2）将正方形 $\text{[math]}$ 绕点D逆时针方向旋转 $\text{[math]}$ ．判断（1）中的结论是否仍然成立？请利用图证明你的结论；
3. （3）在（2）的条件下，若 $\text{[math]}$ ，当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题