 B .
B . 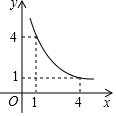 C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
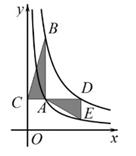
①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1 , y1)、B(x2 , y2)两点在该图象上,且x1+x2=0,则y1=y2。其中说法正确的个数是( )
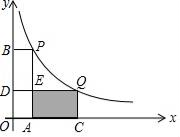

| 面条的总长度y(mm) | 100 | 200 | 400 | 800 | 2000 |
| 面条的粗细s(mm2) | 12.80 | 6.40 | 3.20 | 1.60 | 0.64 |
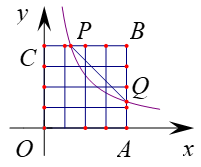
①试直接写出当y1>y2时h的取值范围;
②若y2-y1=3,试求h的值。
因为y= ,即y=﹣
+1,所以我们对比函数y=﹣
来探究.
列表:
| x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ | | 1 | 2 | 3 | 4 | … |
| y=﹣ | … | | | 1 | 2 | 4 | ﹣4 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
| y= | … | | | 2 | 3 | 5 | ﹣3 | ﹣1 | 0 | | | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y= 相应的函数值为纵坐标,描出相应的点,如图所示:
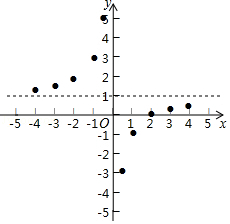
①当x<0时,y随x的增大而;(填“增大”或“减小”)
②y= 的图象是由y=﹣
的图象向平移个单位而得到;
③图象关于点中心对称.(填点的坐标)
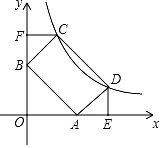
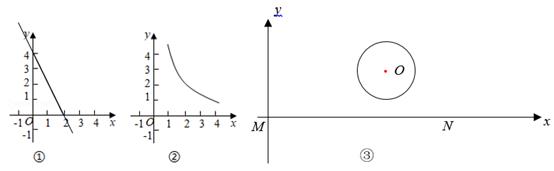
①已知点A(-2,1),则d(O,A)=.
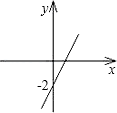
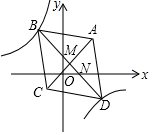
②函数y=-2x+4的图象如图①所示,B是图象上一点,d(O,B)=3,则点B的坐标是.
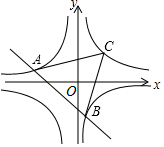
某市要修建一条通往一圆形景观湖的道路,如图③,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边某点P处,如图建立坐标系,圆心O(5,3),半径为 ,求修建道路距离d(O,P)的取值范围.