
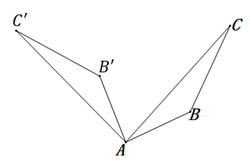
 B .
B . 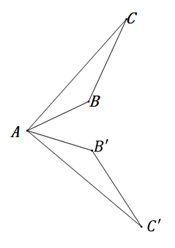 C .
C .  D .
D . 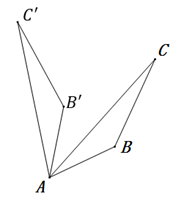

|
投掷次数(n) |
“出现点数为1”的次数(频数m) |
频率 |
| 300 | 52 | 0.173 |
| 400 | 65 | 0.163 |
| 500 | 80 | 0.160 |
| 600 | 99 | 0.165 |
| 700 | 114 | 0.163 |
| 800 | 136 | 0.170 |
| 900 | 151 | 0.168 |
| 1000 | 166 | 0.166 |
根据上表信息,掷一枚骰子,估计“出现点数为1”的概率为(精确到0.001)
|
乘出租车 |
乘坐 公交车 |
乘坐地铁 |
骑共享 单车 |
共需步行 (公里) |
总用时 (分钟) |
费用 (元) |
|
|
方式1 |
√ |
2.0 |
47 |
4 |
|||
|
方式2 |
√ |
56 |
3 |
||||
|
方式3 |
√ |
1.6 |
78 |
3 |
|||
|
方式4 |
√ |
1.8 |
80 |
3 |
|||
|
方式5 |
√ |
√ |
1.5 |
60 |
6 |
||
|
方式6 |
√ |
√ |
1.6 |
56 |
6 |
||
|
方式7 |
√ |
√ |
1.7 |
55 |
6 |
||
|
方式8 |
√ |
√ |
1.5 |
57 |
6 |
||
|
方式9 |
√ |
0.2 |
32 |
41 |
根据表格中提供的信息,小青得出以下四个推断:
①要使费用尽可能少,可以选择方式2,3,4;
②要使用时较短,且费用较少,可以选择方式1;
③如果选择公交车和地铁混合的出行方式,平均用时约57分钟;
④如果将上述出行方式中的“步行”改为“骑共享单车”,那么除方式2外,其它出行方式的费用均会超过8元.
其中推断合理的是(填序号).

求作:菱形ABCD,使其两条对角线的长分别等于线段a,b的长.
作法:①作直线m,在m上任意截取线段 ;
②作线段AC的垂直平分线EF交线段AC于点O;
③以点O为圆心,线段b的长的一半为半径画圆,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的葵形.
![]()
证明: ,
四边形ABCD是 ▲ .
,
四边形ABCD是菱形( ▲ )(填推理的依据).
a.30名同学冬奥知识测试成绩的统计图如下:

b.30名同学冬奥知识测试成绩的频数分布直方图如下(数据分成6组: ,
,
,
):
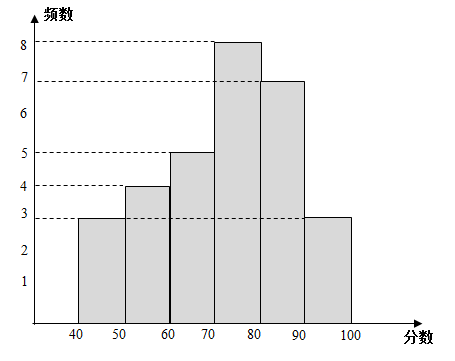
c.测试成绩在 这一组的是:
70 73 74 74 75 75 77 78
d.小明的冬奥知识测试成绩为85分
根据以上信息,回答下列问题:
②若 ,求x1的值(用含a的式子表示);
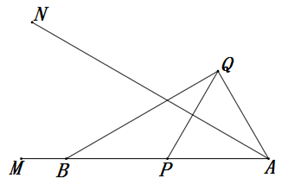
①直接写出 的度数;
②依题意补全图形,并直接写出线段CP与AP的数量关系;

①设 ,求
的大小(用含a的式子表示);
②用等式表示线段 之间的数量关系,并证明.

