
 B .
B .  D .
D . 


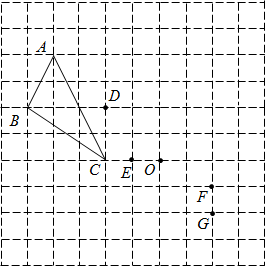
………………甲
………乙
………………………丙
=—2……………………………………丁
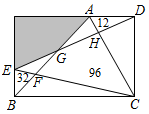
已知:如图,四边形ABCD是菱形,E、F是直线AC上两点,AF=CE .
求证;四边形FBED是菱形.

甲:利用全等,证明四边形FBED四条边相等,进而说明该四边形是菱形;
乙:连接BD , 利用对角线互相垂直的平行四边形是菱形,判定四边形FBED是菱形;
丙:该题目错误,根据已知条件不能够证明该四边形是菱形.


![]()
①这组成绩的中位数是,平均数是;
②该班同学丙因病错过了测试,补测抽到了D“物理”学科,加上丙同学的成绩后,发现这9名同学的成绩的众数与中位数相等,但平均数比①中的平均数大,则丙同学“物理”学科的成绩为.
|
项目 |
A 语文 |
B 数学 |
C 英语 |
D 物理 |
E 历史 |
|
测试人数(人) |
50 |
50 |
50 |
30 |
20 |
|
单科平均成绩(分) |
9 |
8 |
7 |
8 |
9 |

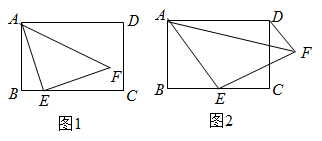

②当抛物线 (c为常数)不存在“相约矩形”,则c的取值范围是.
①当该函数的图象与x轴只有-个交点时,求出交点的坐标;
②我们把平面直角坐标系中横、纵坐标都为整数的点称为“好点”,当抛物线 (a为常数,a>0)的“相约矩形”内部(包括矩形边界)恰有8个“好点”时,直接写出a的取值范围.