浙江省部分学校联考2023-2024学年九年级数学上册开学摸...

更新时间：2023-10-12 浏览次数：39 类型：开学考试

一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. (2024八下·新城期中) 下列新能源汽车标志图案中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·孝昌开学考) 二次根式 $\text{[math]}$ 中，字母a的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·浙江开学考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·浙江开学考) 下列说法正确的是（）

A . 为了解全国中学生的课外阅读情况，应采取全面调查的方式 B . 为了解九年级1200名学生模拟考试的数学成绩，从中抽取200名学生的数学成绩进行调查，这个问题中样本容量为1200 C . 投掷一枚硬币100次，一定有50次“正面朝上” D . 甲、乙两名学生参加“国学小名士”知识竞赛选拔赛成绩的平均数均为94，方差分别为5.3和4.8，则乙学生的成绩稳定

答案解析收藏纠错 + 选题
5. (2023九上·浙江开学考) 点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，则下列各点在此函数图象上的是（）

A . （2，4） B . （-1，-8） C . （-2，-4） D . （4，-2）

答案解析收藏纠错 + 选题
6. (2024九上·孝昌开学考) 据统计，某班7个学习小组上周参加“青年大学习”的人数分别为：5，5，6，6，6，7，7，下列说法错误的是（）

A . 该组数据的中位数是6 B . 该组数据的众数是6 C . 该组数据的平均数是6 D . 该组数据的方差是6

答案解析收藏纠错 + 选题
7. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 相交于点O ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点E ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·杭州开学考)
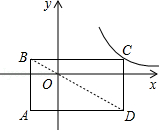
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y= $\text{[math]}$ 的图象上，若点A的坐标为（﹣2，﹣3），则k的值为（　　）

A . 1 B . ﹣5 C . 4 D . 1或﹣5

答案解析收藏纠错 + 选题
9. (2023九上·浙江开学考) 若点 $\text{[math]}$ 与 $\text{[math]}$ 分别是两个函数图象 $\text{[math]}$ 与 $\text{[math]}$ 上的任一点．当 $\text{[math]}$ 时，有-1≤y₁-y₂≤1成立，则称这两个函数在 $\text{[math]}$ 上是“相邻函数”．例如，点 $\text{[math]}$ 与 $\text{[math]}$ 分别是两个函数 $\text{[math]}$ 与 $\text{[math]}$ 图象上的任一点，当 $\text{[math]}$ 时， $\text{[math]}$ ，它在 $\text{[math]}$ 上，-1≤y₁-y₂≤1成立，因此这两个函数在 $\text{[math]}$ 上是“相邻函数”．若函数 $\text{[math]}$ 与 $\text{[math]}$ 在 $\text{[math]}$ 上是“相邻函数”，求a的取值范围（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·浙江开学考) 如图，在矩形内画了一些直线，已知△ADH ， △BEF ，四边形HGFC的面积分别是12、32、96，那么图中阴影部分的面积是（）

A . 48 B . 52 C . 60 D . 108

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2023九上·浙江开学考) “七巧板”是古代中国劳动人民的发明，被誉为“东方魔板”．如图，一只小虫在七巧板上任意爬行，已知它停在这副七巧板上的任何一点的可能性都相同，那么它停在阴影部分的概率是.

答案解析收藏纠错 + 选题
12. (2023九上·浙江开学考) 某超市一月份的营业额为200万元，三月份的营业额为242万元，如果每月比上月增长的百分数相同，设平均每月的增长率为x，则可列方程．

答案解析收藏纠错 + 选题
13. (2023九上·浙江开学考) 在一个不透明的口袋中，装有4个红球和若干个白球，这些球除颜色外其余都相同，如果摸到红球的概率是 $\text{[math]}$ ，那么口袋中有白球个.

答案解析收藏纠错 + 选题
14. (2023九上·浙江开学考) 已知一次函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，则二元一次方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
15. (2023九上·浙江开学考) 如图， $\text{[math]}$ 的顶点A在反比例函数 $\text{[math]}$ 的图象上，点B在y轴上，点C ，点D在 $\text{[math]}$ 轴上，AD与y轴交于点E ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2023九上·浙江开学考) 如图，在平面直角坐标系中，矩形纸片OABC的顶点A ， C分别在x轴，y轴的正半轴上，将纸片沿过点C的直线翻折，使点B恰好落在x轴上的点B′处，折痕交AB于点D ．若OC=9， $\text{[math]}$ ，则折痕CD所在直线的解析式为．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共66分，各小题要求写出必要的解答过程）

17. (2023九上·浙江开学考)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2023九上·浙江开学考) 先化简，再求值， $\text{[math]}$ ；其中a= $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2023九上·浙江开学考) 如图，设反比例函数的解析式为y＝ $\text{[math]}$ （k＞0）．
1. （1）若反比例函数与正比例函数y＝2x的图象有一个交点的纵坐标为2，求k的值；
2. （2）若反比例函数的图象与过点M（-2，0）的直线l：y＝kx+b的图象交于A、B两点，如图，当△ABO的面积为12时，求直线l的解析式．
答案解析收藏纠错 + 选题
20. (2023九上·浙江开学考) 在平面直角坐标系中按要求画图：
1. （1）画出 $\text{[math]}$ 平移后的图形 $\text{[math]}$ ，使点 $\text{[math]}$ 的对应点 $\text{[math]}$ 坐标为 $\text{[math]}$ ．
2. （2）画出 $\text{[math]}$ 关于原点成中心对称的 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023九上·浙江开学考) 某电视台为了解本地区电视节目的收视情况，对部分广州开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了下面两幅不完整的统计图，根据要求回答下列问题：
1. （1）本次问卷调查共调查了名观众；
2. （2）图②中最喜爱“新闻节目”的人数占调查总人数的百分比为，“综艺节目”在扇形统计图中所对应的圆心角的度数为；
3. （3）补全图①中的条形统计图；
4. （4）现有最喜爱“新闻节目”（记为A），“体育节目”（记为B），“综艺节目”（记为C），“科普节目”（记为D）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用列表或画树状图的方法，求出恰好抽到最喜爱“B”和“C”两位观众的概率．
答案解析收藏纠错 + 选题
22. (2023八上·长沙月考) 如图．点A，B，C，D在同一条直线上，点E，F分别在直线 $\text{[math]}$ 的两侧，且 $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

23. (2023九上·浙江开学考) 你的班级正在开展“如何设计拱桥景观灯的悬挂方案”这一数学主题研究活动，请你参加。据以下素材，探索完成任务．

素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 $\text{[math]}$ ，拱顶离水面 $\text{[math]}$ ．据调查，该河段水位在此基础上再涨 $\text{[math]}$ 达到最高．
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂 $\text{[math]}$ 长的灯笼，如图3.为了安全，灯笼底部距离水面不小于 $\text{[math]}$ ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 $\text{[math]}$ ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．

问题解决：

（1）任务1：确定桥拱形状，在图2中建立合适的直角坐标系，求抛物线的函数表达式．
（2）任务2：探究悬挂范围，在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
（3）任务3：拟定设计方案，给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

答案解析收藏纠错 + 选题

24. (2023九上·浙江开学考) 综合与实践：

如图1，已知 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点．
1. （1）观察猜想：
  在图1中，线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；
  
  探究证明：
2. （2）当 $\text{[math]}$ ，把 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针方向旋转到图2的位置，判断 $\text{[math]}$ 的形状，并说明理由；
3. （3）拓展延伸：
  当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，再连接 $\text{[math]}$ ，再取 $\text{[math]}$ 的中点 $\text{[math]}$ ，把 $\text{[math]}$ 绕点 $\text{[math]}$ 在平面内自由旋转，如图3．
  
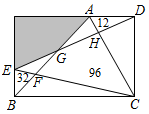
  ①请你判断四边形 $\text{[math]}$ 的形状，并说明理由；
  
  ②四边形 $\text{[math]}$ 面积的最大值为 ▲ ．
答案解析收藏纠错 + 选题