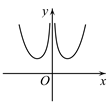
 B .
B . 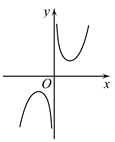 C .
C . 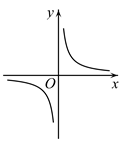 D .
D . 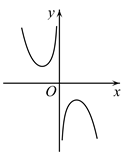
问题:是否存在 ,它的内角
的对边分别为
,且
,
,_________?
注:如果选择多个条件分别解答,按第一个解答计分.
|
所用的时间(单位:天) |
10 |
11 |
12 |
13 |
|
甲生产线的频数 |
10 |
20 |
10 |
10 |
|
乙生产线的频数 |
5 |
20 |
20 |
5 |