一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
二、填空题:本大题共4个小题,每小题5分,共20分。
-
-
-
15.
(2022高一下·梅江月考)
在山顶铁塔上

处测得地面上一点

的俯角

,在塔底

处测得点

的俯角

,已知铁塔

部分高32米,山高

.

-
三、解答题:解答应写出文字说明,证明过程或演算步骤,共70分。
-
-
(1)
求向量

的模长;
-
-
-
(1)
求

在

上的单调增区间;
-
(2)
在角

为锐角的

中,角

、

、

的对边分别为

、

、

,

且

的面积为3,

,求

的值.
-
19.
(2021高一下·大理期中)
某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为

),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为

,三月底测得凤眼莲的覆盖面积为

,凤眼莲的覆盖面积

(单位:

)与月份

(单位:月)的关系有两个函数模型

(

,

)与

(

,

)可供选择。
-
(1)
试判断哪个函数模型更合适并求出该模型的解析式;
-
(2)
求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据:

,

).
-
20.
(2021高一下·大理期中)
已知

内角

、

、

所对的边分别为

、

、

,A为锐角,在以下三个条件中任选一个:①

;②

;③

;并解答以下问题:
-
(1)
若选
▲ (填序号),求

的值;
-
(2)
在(1)的条件下,若

,求

面积

的最大值.
-
-
(1)
求证:

;
-
(2)

与平面

是否平行?试证明你的结论.
-
-
(1)
求

的值;
-
(2)
求

的解析式;
-
(3)
若存在

,使得不等式

成立,求实数

的取值范围.
-
-
(1)
判断幂函数

是否属于集合

?并说明理由;
-
 B .
B . 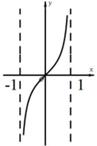 C .
C .  D .
D . 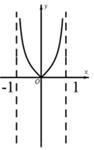

;
是函数
的一条对称轴;
在区间
上为增函数;
在区间
上有四个零点.其中正确命题的序号是( )
时,若
,求
的取值范围;
,都有
,求
的取值范围.