北京市朝阳区部分学校联合2020-2021学年八年级下学期数...

更新时间：2024-07-13 浏览次数：291 类型：期中考试

一、选择题（每小题3分，共24分）

1. (2021八下·朝阳期中) 若二次根式 $\text{[math]}$ 有意义，则下列数中，实数x不可以取的值是（）

A . ﹣1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
2. (2021八下·朝阳期中) △ABC中，已知AB＝1，AC＝2．要使∠B是直角，BC的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八下·朝阳期中) 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是正比例函数y＝kx（k≠0）在第二象限的图象上的两个点，如果P₁点在P₂点左边，那么y₁ ， y₂的大小关系是（）

A . y₁＝y₂ B . y₁＜y₂ C . y₁＞y₂ D . 不能确定

答案解析收藏纠错 + 选题
4. (2022八下·丰润期中) 如图，在四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．要使四边形EFGH为菱形，可以添加的一个条件是（）

A . 四边形ABCD是菱形 B . AC、BD互相平分 C .
AC＝BD
D . AC⊥BD

答案解析收藏纠错 + 选题
5. (2021八下·朝阳期中) 如图，以直角三角形的一条直角边和斜边为一边作正方形M和N，它们的面积分别为9cm²和25cm² ，则直角三角形的面积为（）

A . 6cm² B . 12cm² C . 24cm² D . 3cm²

答案解析收藏纠错 + 选题
6. (2021八下·朝阳期中) 在平面直角坐标系中，一次函数y＝ax+a﹣1（a为常数，且a≠0）的图象一定经过的点是（）

A . （1，1） B . （﹣1，1） C . （﹣1，﹣1） D . （1，﹣1）

答案解析收藏纠错 + 选题
7. (2022八下·孝义期末) 如图，在平面直角坐标系中，已知点A（﹣2，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的正半轴于点C，则点C的横坐标介于（）

A . 0和1之间 B . 1和2之间 C . 2和3之间 D . 3和4之间

答案解析收藏纠错 + 选题
8. (2023八上·包河月考) 甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛，比赛开始时甲在起点，乙在甲的前面200米，他们同时同向出发匀速前进，甲的速度是8米/秒，乙的速度是6米/秒，先到终点者在终点原地等待．设甲、乙两人之间的距离是y米，比赛时间是x秒，当两人都到达终点计时结束，整个过程中y与x之间的函数图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题（本题共有8小题，每小题3分，共24分）

9. (2021八下·朝阳期中) 已知 $\text{[math]}$ ，那么a＝．

答案解析收藏纠错 + 选题
10. (2021八下·望城期末) 已知y是x的一次函数，如表列出了部分对应值，则m＝．

x

0

1

2

y

m

1.5

3.5

答案解析收藏纠错 + 选题
11. (2021八下·朝阳期中) 如图，在△ABC中，∠A＝40°，AB＝AC，点D在AC边上，以CB，CD为边作▱BCDE，则∠E的度数是．

答案解析收藏纠错 + 选题
12. (2021八下·朝阳期中) 如图，点B，C分别是锐角∠A两边上的点，AB＝AC，分别以点B，C为圆心，以AB的长为半径画弧，两弧相交于点D，连接BD，CD．则根据作图过程判定四边形ABCD是菱形的依据是．

答案解析收藏纠错 + 选题
13. (2021八下·朝阳期中) 如图，在矩形ABCD中（AD＞AB），E是BC上一点，且DE＝DA，AF⊥DE，垂足为F．
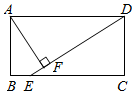
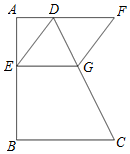
在下列结论中①△AFD≌△DCE；②AF＝ $\text{[math]}$ AD；③AB＝AF；④BE＝AD﹣DF．一定正确的是（把正确的序号写在横线上）．

答案解析收藏纠错 + 选题
14. (2021八下·朝阳期中) 在平面直角坐标系中，已知点A（2，0），直线l₁对应的函数解析式为y＝2x，平移直线l₁使其经过点A，则应向下平移个单位．

答案解析收藏纠错 + 选题
15. (2021八下·朝阳期中) 如图，在平面直角坐标系中，点M是直线y＝﹣x上的动点，过点M作MN⊥x轴，交直线y＝x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为．

答案解析收藏纠错 + 选题
16. (2021八下·朝阳期中) 如图，在平面直角坐标系中，点A、B的坐标分别为（﹣3，3）、（3，5），欲在x轴上找一点P，使PA+PB最短，小白试了四个点（﹣3，0）、（ $\text{[math]}$ ，0）、（0，0）、（3，0）．你认为点P的坐标应该为，PA+PB的最小值为．

答案解析收藏纠错 + 选题

三、按要求解答（17-24题，每小题5分，25-26题，每小题5分，共52分）

17. (2021八下·朝阳期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021八下·朝阳期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，求代数式xy²﹣x²y的值．

答案解析收藏纠错 + 选题
19. (2021八下·朝阳期中) 已知z＝m+y，m是常数，y是x的正比例函数．当x＝2时，z＝1；当x＝3时，z＝﹣1，求z与x的函数关系式．

答案解析收藏纠错 + 选题
20. (2021八下·朝阳期中) 如图，每个小正方形的边长都是1．A、B、C、D均在网格的格点上．
1. （1） ∠BCD是直角吗？请证明你的判断．
2. （2）直接写出四边形ABCD的面积
3. （3）找到格点E，并画出四边形ABED（一个即可），使得其面积与四边形ABCD面积相等．
答案解析收藏纠错 + 选题
21. (2021八下·朝阳期中) 如图，五一期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．

根据以上信息，解答下列问题：
1. （1）设租车时间为x（0＜x≤24）小时，租用甲公司的车所需费用为y₁元，租用乙公司的车所需费用为y₂元，分别求出y₁ ， y₂关于x的函数解析式；
2. （2）请你帮助小明计算选择哪个出游方案合算．
答案解析收藏纠错 + 选题
22. (2021八下·朝阳期中) 已知：如图，点A是直线l外一点，B，C两点在直线l上，∠BAC＝90°，BC＝2BA．
1. （1）按要求作图：（保留作图痕迹）
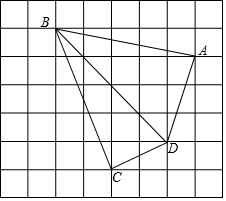
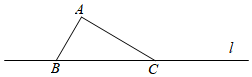
  ①以A为圆心，BC为半径作弧，再以C为圆心，AB为半径作弧，两弧交于点D；
  
  ②作出所有以A，B，C，D为顶点的四边形；
2. （2）比较在（1）中所作出的线段BD与AC的大小关系．
答案解析收藏纠错 + 选题
23. (2021八下·朝阳期中) 四边形ABCD中，∠A＝∠B＝90°，点E在边AB上，点F在AD的延长线上，且点E与点F关于直线CD对称，过点E作EG∥AF交CD于点G，连接FG，DE．
1. （1）求证：四边形DEGF是菱形；
2. （2）若AB＝10，AF＝BC＝8，求四边形DEGF的面积．
答案解析收藏纠错 + 选题
24. (2021八下·朝阳期中) 我们设定，当一条直线与一个正方形的边有两个不同的公共点时，称这条直线与这个正方形相交．如图，在平面直角坐标系中，正方形ABCD的顶点为A（2，1）、B（2，2）、C（1，2）．D（1，1）．
1. （1）判断直线 $\text{[math]}$ 与正方形OABC是否相交，如果是，求出交点，否则说明原因；
2. （2）若直线 $\text{[math]}$ 与正方形OABC相交，求b的取值范围．
答案解析收藏纠错 + 选题
25. (2021八下·朝阳期中) 如图，在正方形ABCD中，点E在边CD上（点E与点C、D不重合），过点E作FG⊥BE，FG与边AD相交于点F，与边BC的延长线相交于点G．
1. （1） BE与FG有什么样的数量关系？请直接写出你的结论：；
2. （2） DF、CG、CE的数量之间具有怎样的关系？并证明你所得到的结论．
3. （3）如果正方形的边长是1，FG＝1.5，直接写出点A到直线BE的距离．
答案解析收藏纠错 + 选题
26. (2021八下·朝阳期中) 在平面直角坐标系XOY中，对于任意三点A，B，C的“矩面积”，给出如下定义：任意两点横坐标差的最大值称为“水平底”a，任意两点纵坐标差的最大值称为“铅垂高”h，“水平底”a与“铅垂高”h的乘积为点A，B，C的“矩面积S”，即“矩面积”S＝ah．
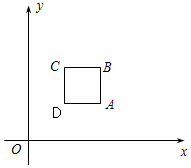
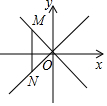
例如：点P（1，2），M（﹣3，1），N（2，﹣2），它们的“水平底”a＝5，“铅垂高”h＝4，“矩面积”S＝ah＝20．
1. （1）已知点A（1，2），B（3，﹣2），C（t，0）．
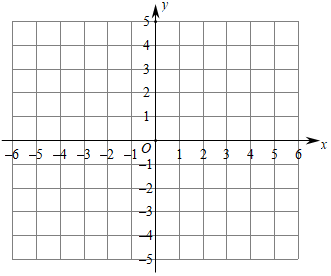
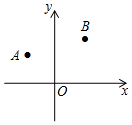
  ①若A，B，C三点的“矩面积”为12，写出点C的坐标：；
  
  ②写出A，B，C三点的“矩面积”的最小值：．
2. （2）已知点D（﹣1，3），E（4，0），F（t，3t），
  ①当D，E，F三点的“矩面积”取最小值时，写出t的取值范围： 0≤t≤1 ；
  
  ②当0≤t≤4时，写出S与t的函数关系式．
答案解析收藏纠错 + 选题