初中数学苏科版八年级上册第六章一次函数单元测试卷

更新时间：2021-06-21 浏览次数：216 类型：单元试卷

一、单选题

1. (2021八上·丹徒期末) 一次函数 $\text{[math]}$ $\text{[math]}$ 的图象过点（0，4），且y随x的增大而增大，则m的值为（）

A . ﹣2 B . ﹣2或2 C . 1 D . 2

答案解析收藏纠错 + 选题
2. (2021八上·淮安期末) 点 $\text{[math]}$ ， $\text{[math]}$ 都在函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
3. (2023八上·合肥期中) 若直线y＝kx+b经过第一、二、四象限，则函数y＝bx－k的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021八上·连云港期末) 已知一次函数 $\text{[math]}$ ，函数值 $\text{[math]}$ 随自变量 $\text{[math]}$ 的增大而减小，那么 m 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020八上·射阳月考) 若k > 4，则一次函数 y = （4 - k）x + k - 4的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2020八上·徐州期末) 若函数 $\text{[math]}$ 的图象如图所示，则关于x的不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八上·淮安期末) 对函数 $\text{[math]}$ ，下列说法正确的是（）

A . 它的图象过点 $\text{[math]}$ B . $\text{[math]}$ 值随着 $\text{[math]}$ 值增大而减小 C . 它的图象经过第二象限 D . 它的图象与 $\text{[math]}$ 轴交于负半轴

答案解析收藏纠错 + 选题
8. (2019八下·沙河期末) 已知一次函数y=kx+b（k≠0），若k+b=0，则该函数的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2021八上·建邺期末) 将函数 $\text{[math]}$ 的图象平移，使它经过点 $\text{[math]}$ ，则平移后的函数表达式是.

答案解析收藏纠错 + 选题
10. (2021八上·建邺期末) 声音在空气中的传播速度 $\text{[math]}$ 与温度 $\text{[math]}$ 的关系如表：

温度（℃）

0

5

10

15

20

速度 $\text{[math]}$

331

336

341

346

351

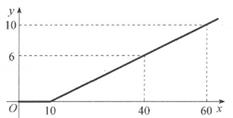
若声音在空气中的传播速度 $\text{[math]}$ 是温度 $\text{[math]}$ 的一次函数；当 $\text{[math]}$ 时，声音的传播速度为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
11. (2022七上·河口期末) 已知点P（a，b）在一次函数y＝2x﹣1的图象上，则4a﹣2b+1＝.

答案解析收藏纠错 + 选题
12. (2021八上·宝应期末) 对于函数 $\text{[math]}$ ，有下列性质：①它的图象过点 $\text{[math]}$ ，② $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小，③与 $\text{[math]}$ 轴交点为 $\text{[math]}$ ，④它的图象不经过第二象限，其中正确的序号是（请填序号）.

答案解析收藏纠错 + 选题
13. (2021八上·泰州期末) 在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点.已知点A（0，4），点B（a，0）是x轴正半轴上的点，若△AOB内部（不包括边界）的整点个数为6，则 a的取值范围是.

答案解析收藏纠错 + 选题
14. (2021八上·靖江期末) 已知一次函数 $\text{[math]}$ ，若y随x的增大而减小，则k的取值范围是.

答案解析收藏纠错 + 选题
15. (2021八上·靖江期末) 已知一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 和 $\text{[math]}$ ，那么 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
16. (2021八上·海州期末) 在一次函数y=（k﹣3）x+2中，y随x的增大而减小，则k的取值.

答案解析收藏纠错 + 选题
17. (2021八上·海州期末) 如图所示的折线 $\text{[math]}$ 为某地向香港地区打电话需付的通话费y（元）与通话时间 $\text{[math]}$ 之间的函数关系，则通话 $\text{[math]}$ 应付通话费元.

答案解析收藏纠错 + 选题
18. (2021八上·兴化期末) 已知点 $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图像上，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
19. (2020八上·射阳月考) 点 $\text{[math]}$ ， $\text{[math]}$ 是直线 $\text{[math]}$ 上的两点，则 $\text{[math]}$ 0（填“＞”或“＜”）.

答案解析收藏纠错 + 选题
20. (2020八下·江苏月考) 如图，一次函数y＝kx＋b的图象经过点A（0，3），B（4，﹣3），则关于x的不等式kx＋b＋3＜0的解集为.

答案解析收藏纠错 + 选题

三、解答题

21. (2020八下·通州月考) 如图，在靠墙（墙长为18m）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，如果竹篱笆总长为35m，求鸡场的长y （m）与宽x （m）的函数关系式，并求自变量的取值范围.

答案解析收藏纠错 + 选题
22. (2020八上·苏州期末) 某长途客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需支付相应的行李费。设x表示行李的质量(kg)，y表示行李费(元)，y与x的函数关系如图所示，请写出x、y变化过程中的实际意义。

答案解析收藏纠错 + 选题
23. (2023八上·宁波期末) 市场上甲种商品的采购价为60元/件，乙种商品的采购价为100元/件，某商店需要采购甲、乙两种商品共15件，且乙种商品的件数不少于甲种商品件数的2倍．设购买甲种商品 $\text{[math]}$ 件（ $\text{[math]}$ >0），购买两种商品共花费 $\text{[math]}$ 元．
1. （1）求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式（写出自变量 $\text{[math]}$ 的取值范围）；
2. （2）试利用函数的性质说明，当采购多少件甲种商品时，所需要的费用最少？
答案解析收藏纠错 + 选题
24. (2019八下·来宾期末) 某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费y（元）是行李质量x（kg）的一次函数．已知行李质量为20kg时需付行李费2元，行李质量为50kg时需付行李费8元．
1. （1）当行李的质量x超过规定时，求y与x之间的函数表达式；
2. （2）求旅客最多可免费携带行李的质量．
答案解析收藏纠错 + 选题
25. 为调动销售人员的积极性，A、B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金．已知A、B公司两位销售员小李、小张1～6月份的销售额如下表：
月份
销售额
销售额（单位：元）
1月
2月
3月
4月
5月
6月
小李（A公司）
11600
12800
14000
15200
16400
17600
小张（B公司
7400
9200
11000
12800
14600
16400
（1）请问小李与小张3月份的工资各是多少？
（2）小李1～6月份的销售额y₁与月份x的函数关系式是y₁=1200x+10400，小张1～6月份的销售额y₂也是月份x的一次函数，请求出y₂与x的函数关系式；
（3）如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资．

答案解析收藏纠错 + 选题
26.
某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需要购买行李票．已知行李费y（元）是行李质量x（kg）之间的函数表达式为y=kx+b．这个函数的图象如图所示：
（1）求k和b的值；
（2）求旅客最多可免费携带行李的质量；
（3）求行李费为4～15元时，旅客携带行李的质量为多少？

答案解析收藏纠错 + 选题

四、综合题

27. (2022八上·雁塔期中) 甲、乙两个探测气球分别从海拔 $\text{[math]}$ 和 $\text{[math]}$ 处同时出发，匀速上升 $\text{[math]}$ .下图是甲、乙两个探测气球所在位置的海拔y（单位：m）与气球上升时间x（单位： $\text{[math]}$ ）的函数图象.
1. （1）求这两个气球在上升过程中y关于x的函数解析式；
2. （2）当这两个气球的海拔高度相差 $\text{[math]}$ 时，求上升的时间.
答案解析收藏纠错 + 选题
28. (2021八上·丹阳期末) 某地区的电力资源缺乏，未能得到较好的开发.该地区一家供电公司为了居民能节约用电，采用分段计费的方法来计算电费.月用电量 $\text{[math]}$ （度）与相应电费 $\text{[math]}$ （元）之间的函数图象如图所示.
1. （1）月用电量为 $\text{[math]}$ 度时，应交电费多少元？
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
3. （3）月用电量为 $\text{[math]}$ 度时，应交电费多少元？
答案解析收藏纠错 + 选题
29. (2021八上·宝应期末) 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象由函数 $\text{[math]}$ 的图象平移得到，且经过点 $\text{[math]}$ .
1. （1）请在所给平面直角坐标系中画出这个一次函数的图象并求该一次函数的解析式；
2. （2）当 $\text{[math]}$ 时，对于 $\text{[math]}$ 的每一个值函数 $\text{[math]}$ （ $\text{[math]}$ ）的值大于一次函数 $\text{[math]}$ 的值，求出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
30. (2021八上·淮安期末) 甲汽车出租公司按每千米1.5元收取租车费；乙汽车出租公司按每千米0.5元收取租车费，另加管理费800元.设用车里程为 $\text{[math]}$ 千米.租用甲、乙两家公司的汽车费用分别为 $\text{[math]}$ 元、 $\text{[math]}$ 元.
1. （1）分别求出 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）问当 $\text{[math]}$ 为何值时，租用甲公司的汽车费用和租用乙公司的汽车费一样多？
答案解析收藏纠错 + 选题
31. (2020八下·通山期末) 甲、乙两家商场平时以同样的价格出售相同的商品.“五一”期间两家商场都让利酬宾，其中甲商场所有商品按 $\text{[math]}$ 折出售，乙商场对一次购物中超过 $\text{[math]}$ 元后的价格部分打 $\text{[math]}$ 折.设 $\text{[math]}$ （单位：元）表示商品原价， $\text{[math]}$ （单位：元）表示在甲商场购物金额， $\text{[math]}$ （单位：元）表示在乙商场购物金额.
1. （1）就两家商场的让利方式分别写出 $\text{[math]}$ 关于x的函数解析式；
2. （2） y_甲关于x的函数图象如图所示，请在同一直角坐标系中画出 $\text{[math]}$ 关于x的函数图象；
3. （3） “五一”期间，如何选择这两家商场去购物更省钱？
答案解析收藏纠错 + 选题
32. (2021八上·泰州期末) 某长途汽车客运公司规定旅客可以免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 $\text{[math]}$ ，这个函数的图象如图所示，求：
1. （1） k和b的值；
2. （2）旅客最多可免费携带行李的质量；
3. （3）行李费为4~15元时，旅客携带行李的质量为多少？
答案解析收藏纠错 + 选题
33. (2021八上·泰州期末) 如图1，甲、乙两个容器内都装了一定数量的水，现将甲容器中的水匀速倒入乙容器中. 图2中，线段AB、线段CD分别表示容器中的水的深度h（厘米）与倒入时间t（分钟）的函数图象.
1. （1）请说出点C的纵坐标的实际意义；
2. （2）经过多长时间，甲、乙两个容器中的水的深度相等？
3. （3）如果甲容器的底面积为10cm² ，求乙容器的底面积.
答案解析收藏纠错 + 选题
34. (2021八下·阿拉善盟期末) 剧院举行新年专场音乐会，成人票每张20元，学生票每张5元，剧院制定了两种优惠方案，方案1：购买一张成人票赠送一张学生票；方案2：按总价的 $\text{[math]}$ 付款.某校有4名老师与若干名（不少于4人）学生听音乐会.
1. （1）设学生人数为x（人），付款总金额为y（元），分别表示这两种方案；
2. （2）请计算并确定出最节省费用的购票方案.
答案解析收藏纠错 + 选题
35. (2021八上·海州期末) 甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走.设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数函数图象的一部分如图所示.
1. （1）求甲行走的速度；
2. （2）在坐标系中，补画s关于t函数图象的其余部分；
3. （3）问甲、乙两人何时相距360米？
答案解析收藏纠错 + 选题
36. (2021八上·兴化期末) 供销商场购进甲、乙两种洗衣机共80台进行销售，其中乙洗衣机的数量不超过甲洗衣机的3倍，甲洗衣机每台利润为500元，乙洗衣机每台利润为600元．设购进甲洗衣机 $\text{[math]}$ （台），这80台洗衣机全部售出的总利润为 $\text{[math]}$ （元）．
1. （1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式；
2. （2）当甲洗衣机购进多少台时，销售总利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
37. (2021·苏州模拟) 某技工培训中心有钳工 $\text{[math]}$ 名、车工 $\text{[math]}$ 名．现将这 $\text{[math]}$ 名技工派往 $\text{[math]}$ 两地工作，设派往 $\text{[math]}$ 地 $\text{[math]}$ 名钳工，余下的技工全部派往 $\text{[math]}$ 地，两地技工的月工资情况如下表：

钳工/（元/月）

车工/（元/月）

$\text{[math]}$ 地

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$ 地

$\text{[math]}$

$\text{[math]}$
1. （1）试写出这 $\text{[math]}$ 名技工的月工资总额 $\text{[math]}$ （元）与 $\text{[math]}$ （名）之间的函数表达式，并写出 $\text{[math]}$ 的取值范围；
2. （2）根据预算，这 $\text{[math]}$ 名技工的月工资总额不得超过 $\text{[math]}$ 元．当派往 $\text{[math]}$ 地多少名钳工时，这些技工的月工资总额最大？月工资总额最大为多少元？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

初中数学苏科版八年级上册第六章一次函数单元测试卷

副标题：

*注意事项：

初中数学苏科版八年级上册第六章一次函数单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

温度（℃）	0	5	10	15	20
速度 $\text{[math]}$	331	336	341	346	351

月份销售额	销售额（单位：元）
月份销售额	1月	2月	3月	4月	5月	6月
小李（A公司）	11600	12800	14000	15200	16400	17600
小张（B公司	7400	9200	11000	12800	14600	16400

	钳工/（元/月）	车工/（元/月）
$\text{[math]}$ 地	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 地	$\text{[math]}$	$\text{[math]}$

小学

初中

高中

初中数学苏科版八年级上册第六章 一次函数 单元测试卷

副标题：

*注意事项：

初中数学苏科版八年级上册第六章 一次函数 单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

初中数学苏科版八年级上册第六章一次函数单元测试卷

初中数学苏科版八年级上册第六章一次函数单元测试卷