



平移、旋转和翻折是初中阶段三大基本几何变换.平移、旋转或翻折后的图形与原图形全等,所以我们又把这些几何变换称之保形变换.我市某校数学思维社团成员在学习了平面直角坐标系及一次函数以后,尝试在平面直角坐标系中研究几何变换.
本着简单到复杂的原则,他们先研究了点的变换:已知平面内一点 .
①将点 向左平移
个单位,平移后点
的坐标为 ;
②点 关于直线
的对称点的坐标为;
③将点 绕点
旋转
,旋转后点
的坐标为;
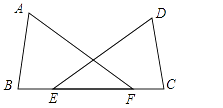
数学思维社团成员认为线的变换只要抓住一些关键点的变换就可以了.已知如图,直线 分别与
轴、
轴交于点
两点,直线
交直线
于点
.

①直线 向右平移
个单位,平移后的直线表达式为;
②将直线 沿直线
翻折,翻折后的直线表达式为;
③将直线 绕点
旋转
,旋转后的直线表达式为 ;
④将直线 绕点
逆时针旋转
,添加一个你认为合适的角度
;并直接写出旋转后的直线表达式 .
如果 条线段将一个三角形分成
个等腰三角形,那么这
条线段就称为这个三角形的“二分等腰线”,如果
条线段将一个三角形分成
个等腰三角形,那么这
条线段就称为这个三角形的“三分等腰线”.
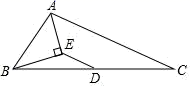
如图(1),在 中,
,请你在这个三角形中画出它的“二分等腰线”,不限作法,请在图中标出等腰三角形顶角的度数.


小明在学习了上面的材料后得到一个结论:直角三角形一定存在“二分等腰线”;而小丽则认为直角三角形也一定存在“三分等腰线”.
①你认为直角三角形的 就是它的“二分等腰线”;
②如图(3),在 中,
,请你在图(3)中帮助小丽画出
的“三分等腰线”(要求:尺规作图,不写作法,保留作图痕迹).
