 B .
B .  C .
C .  D .
D . 
 B .
B . 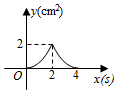 C .
C .  D .
D . 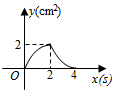

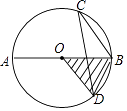
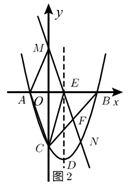
①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )


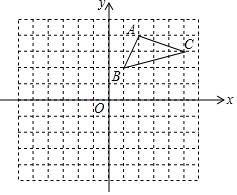
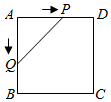
(1)以点(0,0)为旋转中心,将△ABC顺时针转动90°,得到△A1B1C1 , 在坐标系中画出△A1B1C1 , 写出A1、B1、C1的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),直接写出对应点P1的坐标.
(3)作出△ABC关于点O的中心对称图形△A2B2C2.
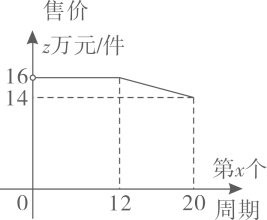

①试说明: .
②判断直线 与
的位置关系,并说明理由.


①证明:四边形 为菱形.
② .