
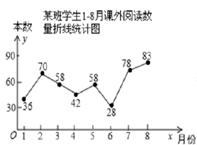
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 

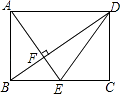




如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B , D , E在同一直线上,连接AD , BD .
①请探究AD与BD之间的位置关系?并加以证明.
②若AC=BC= ,DC=CE=
,求线段AD的长.
如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC= ,BC=
,CD=
,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD , 连接AD , 当点B , D , E在同一直线上时,画出图形,并求线段AD的长.
