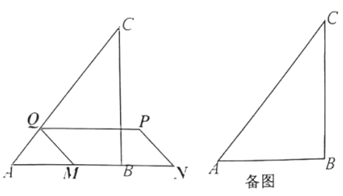
 B .
B .  C .
C .  D .
D . 
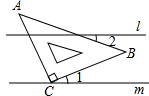
 B .
B . 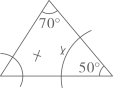 C .
C . 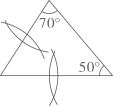 D .
D . 



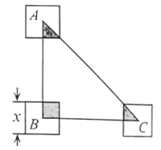
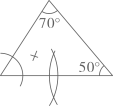
 B .
B . 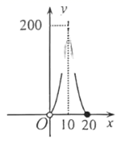 C .
C .  D .
D . 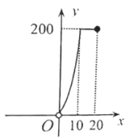
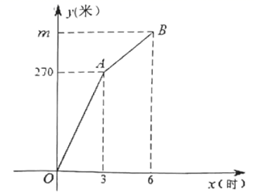
②求代数式 的值;
①当购买苹果和梨的重量相等时,最多能够买多少千克苹果?(千克只取整数)
②当购买苹果的重量是梨的重量的2倍时,最多能够买多少千克苹果?(千克只取整数)
|
| | | |
| | 3 | 0.8 | 1.2 |
| | 0.24 | 0.3 | 2.46 |
| | 0.32 | 0.28 | 1.4 |
试估计“可回收垃圾”投放正确的概率.
①求 的半径
;
②直接写出图中阴影部分的周长.
②求自变量 的取值范围;