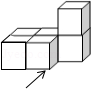
 B .
B . 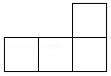 C .
C . 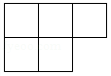 D .
D . 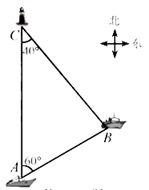
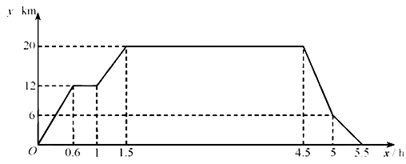
已知学校、书店、陈列馆依次在同一条直线上,书店离学校 ,陈列馆离学校
.李华从学校出发,匀速骑行
到达书店;在书店停留
后,匀速骑行
到达陈列馆;在陈列馆参观学习一段时间,然后回学校;回学校途中,匀速骑行
后减速,继续匀速骑行回到学校.给出的图象反映了这个过程中李华离学校的距离
与离开学校的时间
之间的对应关系.
请根据相关信息,解答下列问题:
|
离开学校的时间/ | | | | | |
| 离学校的距离/ | 2 | 12 |
①书店到陈列馆的距离为 ;
②李华在陈列馆参观学的时间为h;
③李华从陈列馆回学校途中,减速前的骑行速度为 ;
④当李华离学校的距离为 时,他离开学校的时间为h.
(Ⅰ)当 时,求该抛物线的顶点坐标;
(Ⅱ)当 时,点
,若
,求该抛物线的解析式;
(Ⅲ)当 时,点
,过点C作直线l平行于x轴,
是x轴上的动点,
是直线l上的动点.当a为何值时,
的最小值为
,并求此时点M,N的坐标.