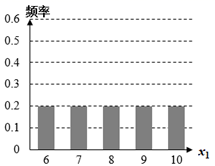
 B .
B . 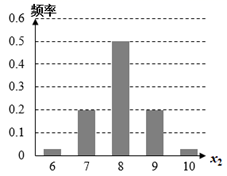 C .
C . 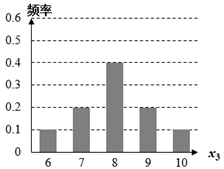 D .
D . 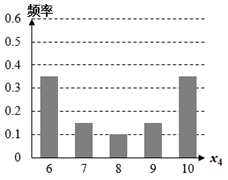
 B .
B . 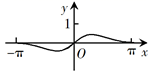 C .
C . 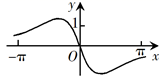 D .
D . 


| | 5 | 6 | 7 | 8 | 9 | 10 |
| | 0.4 | 3.5 | 5.2 | 7.0 | 8.6 | 10.7 |
| | -0.6 | 0.54 | 0.28 | 0.12 | -0.24 | -0.1 |
| | -0.63 | 1.71 | 2.10 | 1.63 | -0.7 | -5.42 |
(剔除数据前的参考数据: ,
,
,
,
,
,
,
,
.)参考公式:
,
.

求证:点 在定圆上.