河北省保定师范附属学校2020-2021学年八年级下学期数学...

更新时间：2024-07-31 浏览次数：122 类型：期中考试

一、单选题

1. (2021八下·保定期中) 不等式x＞1在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021八下·保定期中) 若 $\text{[math]}$ ，则下列各式中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八下·保定期中) 下列图形既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022八下·重庆市期中) 下列各式由左边到右边的变形中，是分解因式的是（）

A . （a－3）（a＋3）＝a²－9 B . x²＋x－5＝（x－2）（x＋3）＋1 C . x²＋1＝x（x＋ $\text{[math]}$ ） D . a²b＋ab²＝ab（a＋b）

答案解析收藏纠错 + 选题
5. (2021九上·龙江期末) 如图，将含有 $\text{[math]}$ 锐角的三角板 $\text{[math]}$ 绕 $\text{[math]}$ 的锐角顶点 $\text{[math]}$ 逆时针旋转一个角度到 $\text{[math]}$ ，若 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，则旋转角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八下·保定期中) 如图，点A（0，8）， $\text{[math]}$ AOB沿x轴向右平移后得到 $\text{[math]}$ ，点A的对应点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，则 $\text{[math]}$ AOB向右平移的长度为（）

A . $\text{[math]}$ B . 10 C . 8 D . 6

答案解析收藏纠错 + 选题
7. (2021八下·保定期中) 如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交X轴于点M，交Y轴于点N，再分别以点M、N为圆心，大于 $\text{[math]}$ MN的长为半径画弧，两弧在第二象限交于点P.若点P的坐标为（3a－1，b），则a与b的数量关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·保定期中) m、n是常数，若 $\text{[math]}$ 的解是 $\text{[math]}$ ，则 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021八下·保定期中) 若实数x满足x²﹣2x﹣1＝0，则2x³﹣7x²+4x+2023的值为（）

A . 2020 B . 2021 C . 2022 D . 2023

答案解析收藏纠错 + 选题
10. (2021八下·保定期中) 下列多项式能用完全平方公式分解因式的是（）

A . x²﹣2x﹣1 B . （a+b）（a﹣b）﹣4ab C . a²+ab+ $\text{[math]}$ b² D . y²+2y﹣1

答案解析收藏纠错 + 选题
11. (2021八下·保定期中) 定义： $\text{[math]}$ 为平面直角坐标系内的点，若满足 $\text{[math]}$ ，则把点A叫做“平衡点”，例如： $\text{[math]}$ ， $\text{[math]}$ 都是平衡点．当 $\text{[math]}$ 时，直线 $\text{[math]}$ 上有“平衡点”，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021八下·保定期中) 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别对应下列六个字，师、爱、我、保、好、美，现将 $\text{[math]}$ 因式分解．结果呈现的密码信息可能是（）

A . 我爱美 B . 保师好 C . 爱我保师 D . 美我保师

答案解析收藏纠错 + 选题
13. (2023八下·南海期中) 如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）

A . 点M B . 格点N C . 格点P D . 格点Q

答案解析收藏纠错 + 选题
14. (2021八下·保定期中) 如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：
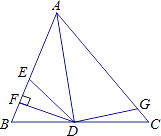
①BD=CE；②∠ABD+∠ECB=45°；③BD⊥CE；④BE²=2（AD²+AB²）﹣CD² ．其中正确的是（）

A . ①②③④ B . ②④ C . ①②③ D . ①③④

答案解析收藏纠错 + 选题
15. (2021八上·大石桥月考) 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）

A . 11 B . 5.5 C . 7 D . 3.5

答案解析收藏纠错 + 选题
16. (2021八下·保定期中) 如图，等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 边在直线 $\text{[math]}$ 上，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转到位置可得到点 $\text{[math]}$ ，此时 $\text{[math]}$ ；将①位置的三角形绕点 $\text{[math]}$ 顺时针旋转到②位置，可得到点 $\text{[math]}$ ，此时 $\text{[math]}$ ；将②位置的三角形绕点 $\text{[math]}$ 顺时针旋转到③位置，可得到点 $\text{[math]}$ ，此时 $\text{[math]}$ ；…，按此规律垂线旋转，直至得到点 $\text{[math]}$ 为止，则 $\text{[math]}$ （）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

17. (2021八下·保定期中) 某种药品的说明书上，贴有如图所示的标签．一次服用这种药品的剂量范围是mg~mg

用法用量：口服，每天 $\text{[math]}$ ，分2～3次服用

规格：□□□□□□

贮藏：□□□□□□

答案解析收藏纠错 + 选题
18. (2021八下·保定期中) 已知x，y满足方程组 $\text{[math]}$ ，则 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
19. (2021八下·保定期中) 如图，已知 $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，点O是 $\text{[math]}$ 的中点，点D在射线 $\text{[math]}$ 上，连结 $\text{[math]}$ ，则 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值=．

答案解析收藏纠错 + 选题

三、解答题

20. (2021八下·保定期中) 计算题：
1. （1）解不等式组 $\text{[math]}$ ，并写出它的整数解．
2. （2）利用因式分解计算：
  ① $\text{[math]}$ ；
  
  ② $\text{[math]}$ ；
  
  ③ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2021八下·保定期中)
如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．
1. （1）请画出△ABC关于原点对称的△A₁B₁C₁ ，并写出A₁的坐标；
2. （2）请画出△ABC绕点B逆时针旋转90°后的△A₂B₂C₂ ．
答案解析收藏纠错 + 选题
22. (2021八下·保定期中) 如图①，△ABC中，∠ABC，∠ACB的平分线交于O点，过O点作BC平行线交AB，AC于E，F．
1. （1）试说明：EO＝BE；
2. （2）探究图①中线段EF与BE，CF间的关系，并说明理由；
3. （3）探究图②，△ABC中若∠ABC的平分线与△ABC的外角平分线交于O，过点O作BC的平行线交AB于E，交AC于F，这时EF与BE，CF的关系又如何？请直接写出关系，不需要说明理由．
答案解析收藏纠错 + 选题
23. (2021八下·保定期中) 如图，在平面直角坐标系中，一次函数y＝﹣x+n图象与正比例函数y＝2x的图象交于点A（m，4）．
1. （1）求m，n的值；
2. （2）设一次函数y＝﹣x+n的图象与x轴交于点B，与y轴交于点C，求点B，点C的坐标；
3. （3）直接写出使函数y＝﹣x+n的值小于函数y＝2x的值的自变量x的取值范围．
4. （4）在x轴上是否存在点P使△PAB为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
24. (2021八下·保定期中) 阅读下列材料：
解答“已知 $\text{[math]}$ ，且 $\text{[math]}$ ，试确定 $\text{[math]}$ 的取值范围”有如下解法

解：∵ $\text{[math]}$ ，∴ $\text{[math]}$ ，又∵ $\text{[math]}$ ，∴ $\text{[math]}$ ，∴ $\text{[math]}$

又∵ $\text{[math]}$ ，∴ $\text{[math]}$ ． ①

同理可得 $\text{[math]}$ ②

由①+②得： $\text{[math]}$ ，∴ $\text{[math]}$ 的取值范围是 $\text{[math]}$

按照上述方法，完成下列问题：
1. （1）已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是．
2. （2）已知关于x，y的方程组 $\text{[math]}$ 的解都是正数
  ①求a的取值范围；
  
  ②若 $\text{[math]}$ 且 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
25. (2021八下·保定期中) 春节前夕，某批发部从厂家购进A、B两种礼盒，已知购进2个A礼盒和3个B礼盒共花520元；购进3个A礼盒和2个B礼盒共花费480元．
1. （1）求A、B两种礼盒的单价分别是多少元？
2. （2）该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个，B种礼盒的数量不超过A种礼盒数量的2倍，共有几种进货方案？
3. （3）已知销售一个A种礼盒可获利10元，销售一个B种礼盒可获利18元，该店主决定每售出一个B种礼盒，为爱心公益基金捐款m元，每个A种礼盒的利润不变，在（2）的条件下，要使A、B两种礼盒全部售出后所有方案获利均相同，m的值应是多少？此时这个批发部获利多少元？
答案解析收藏纠错 + 选题
26. (2021八下·保定期中) 回答下列问题：
1. （1）（发现）如图1，点 $\text{[math]}$ 为线段 $\text{[math]}$ 外一动点，且 $\text{[math]}$ ， $\text{[math]}$ ．
  填空：线段 $\text{[math]}$ 的最大值为．
2. （2）（应用）点 $\text{[math]}$ 为线段 $\text{[math]}$ 外一动点，且 $\text{[math]}$ ， $\text{[math]}$ ，如图2所示，分别以 $\text{[math]}$ ， $\text{[math]}$ 为边，作等腰直角 $\text{[math]}$ 和等腰直角 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
  
  ①证明： $\text{[math]}$ ．
  
  ②求线段 $\text{[math]}$ 的最大值．
3. （3）（拓展）如图3，在平面直角坐标系中，直线 $\text{[math]}$ ； $\text{[math]}$ 与坐标轴交于点 $\text{[math]}$ 、 $\text{[math]}$ 两点，点 $\text{[math]}$ 为线段 $\text{[math]}$ 外一动点，且 $\text{[math]}$ ，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ，连接 $\text{[math]}$ ，求线段 $\text{[math]}$ 长的最大值并直接写出此时点 $\text{[math]}$ 的横坐标．
答案解析收藏纠错 + 选题