黑龙江省齐齐哈尔富拉尔基区2021年中考数学模拟试卷

更新时间：2021-07-29 浏览次数：112 类型：中考模拟

一、单选题

1. (2021七上·新化期中) ﹣2021的相反数的倒数是（）

A . ﹣2021 B . $\text{[math]}$ C . $\text{[math]}$ D . 2021

答案解析收藏纠错 + 选题
2. (2021·富拉尔基模拟) 下列“数字图形”中，即是轴对称图形，又是中心对称图形的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2021·富拉尔基模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ ³＝﹣6x⁶ C . x²＋x²＝2x⁴ D . （x²）⁴＝x⁸

答案解析收藏纠错 + 选题
4. (2021·富拉尔基模拟) 齐齐哈尔市某学校开展为贫困山区捐赠棉衣活动，以下是其中五个班级捐赠棉衣数量：40，20，x ， 90，20，已知这组数据的平均数40，则这组数据的中位数和众数分别是（）

A . 30和20 B . 40和20 C . 20和20 D . 20和30

答案解析收藏纠错 + 选题
5. (2021·富拉尔基模拟) 将一副直角三角尺，按如图所示位置摆放，使30°角所对的直角边和含45°角的三角尺的直角边放在同一条直线上，则∠1的度数是（）

A . 45° B . 60° C . 75° D . 85°

答案解析收藏纠错 + 选题
6. (2024九下·茂名月考) 如图，P是菱形ABCD边上的一动点，它从点A出发沿A→B→C的路径匀速运动到点C ，点R 是 CD边的中点，点M ，点N分别是线段AP ， PR的中点，设P点运动时间为x ， MN的长为y ，则y关于x的函数图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021·富拉尔基模拟) 如图，由一些大小相同的小正方体搭成的几何体的左视图和主视图如图所示，则搭成该几何体的小正方体的个数最少是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
8. (2021·富拉尔基模拟) 一个不透明的盒子里有若干个黑球和3个白球，3个红球，它们除颜色外没有其他区别，若从这个盒子里随机摸出一个黑球的概率是 $\text{[math]}$ ，则这个盒子里黑球的个数为（）

A . 12个 B . 9个 C . 6个 D . 3个

答案解析收藏纠错 + 选题
9. (2021·富拉尔基模拟) 疫情防控期间，某社区决定用1000元订购A ， B两种型号口罩（两种口罩都买），其中A种型号口罩每包80元，B种型号口罩每包120元，则可供社区选择的购买方案有（）

A . 4种 B . 5种 C . 6种 D . 7种

答案解析收藏纠错 + 选题
10. (2021·富拉尔基模拟) 如图，抛物线y＝ax²＋bx＋c（a≠0）交x轴于点A（﹣1，0），对称轴为x＝1，与x轴的另一个交点为B ，点C为抛物线顶点．下列结论：①abc＜0；②4a＋2b＋c＞0；③a＋b＞0；④c＜4b；⑤若△ABC是等腰三角形时，a＝ $\text{[math]}$ ．其中结论正确的有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题

11. (2021七上·虎林期末) 2020年，面对严峻复杂的国内外环境，特别是新冠肺炎疫情的巨大冲击，在党中央坚强领导下，我省发展质量稳步提升，人民生活持续改善，龙江全面振兴全方位振兴取得新的重大进展．初步核算，2020年全省实现地区生产总值13698.5亿元，把13698.5亿元，用科学记数法表示为元．

答案解析收藏纠错 + 选题
12. (2021·富拉尔基模拟) 如图，在四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试添加一个条件：，使四边形 $\text{[math]}$ 为矩形．

答案解析收藏纠错 + 选题
13. (2021·富拉尔基模拟) 一个圆锥的底面半径为3cm，将其侧面展开得到扇形圆心角为216°，则此圆锥的高为．

答案解析收藏纠错 + 选题
14. (2021·富拉尔基模拟) 已知关于x的分式方程 $\text{[math]}$ 的解是非负数，则m的取值范围是．

答案解析收藏纠错 + 选题
15. (2021·富拉尔基模拟) 如图，在平面直角坐标系中，矩形ABCD的顶点A在x轴负半轴上，顶点C在y轴正半轴上，点B（4，6），AB＝10，若反比例函数 $\text{[math]}$ 的图象经过点D ，则k的值为．

答案解析收藏纠错 + 选题
16. (2021·富拉尔基模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为边作等腰直角 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
17. (2021·富拉尔基模拟) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与x轴交于点A与y轴交于点B ，点O为坐标原点，C₁为AB中点，过C₁作C₁A₁⊥OA于点A₁ ，连接OC₁ ， △OA₁C₁面积记为S₁；C₂为AC₁中点，过C₂作C₂A₂⊥OA于点A₂ ，连接OC₂ ， △OA₂C₂面积记为S₂；C₃为AC₂中点，过C₃作C₃A₃⊥OA于点A₃ ，连接OC₃ ， △OA₃C₃面积记为S₃……以此类推，面积为S₂₀₂₁为．

答案解析收藏纠错 + 选题

三、解答题

18. (2021·富拉尔基模拟)
1. （1）计算： $\text{[math]}$
2. （2）分解因式：ax²－9ay²
答案解析收藏纠错 + 选题
19. (2021九上·顺德月考) 解方程：2x²＝3x－1

答案解析收藏纠错 + 选题
20. (2021·富拉尔基模拟) 2021年5月11日，国家统计局发布《第七次全国人口普查公报》，为调查初中学生对人口普查意义和普查数据的了解程度，某区从7、8、9年级学生中各随机抽取100人进行线上问卷调查，将这些同学调查问卷成绩按：A清楚了解；B基本了解；C完全不了解，这三个等级进行统计，被抽测的八年级学生成绩为C等级的人数为2人，被抽测的七年级和九年级学生B等级的人数相等，调查人员根据所得数据绘制成如下两幅不完整的统计图．
请根据相关信息，解答下列问题：
1. （1） C等级人数占总抽测人数的扇形统计图的圆心角的度数为；
2. （2）求被抽取的八年级学生成绩为A等级的人数，并补全条形统计图；
3. （3）被抽取的七年级学生中，成绩为C等级的人数为人；
4. （4）本区九年级共有学生1200人，由此次调查数据估计，全区九年级学生中成绩为C等级的人数．
答案解析收藏纠错 + 选题
21. (2021·富拉尔基模拟) 如图，AB是⊙O的弦，点C是 $\text{[math]}$ 的中点，连接BC ，过点A作AD∥BC交⊙O于点D ，连接CD ，延长DA至E ，连接CE ，使CD＝CE ．
1. （1）求证：CE是⊙O的切线；
2. （2）若AB＝9，AE＝6，求AD的长．
答案解析收藏纠错 + 选题
22. (2021八下·富拉尔基期末) 在一条公路上依次有A ， B ， C三地，甲车从A地出发，驶向C地，同时乙车从C地出发驶向B地，到达B地停留1小时后，按原路原速返回C地，两车匀速行驶，甲车比乙车晚1小时到达C地．两车距各自出发地的路程y（千米）与时间x（小时）之间的函数关系如图所示．请结合图象信息解答下列问题：
1. （1）甲车行驶速度是千米/小时，A ， B两地的路程为千米；
2. （2）求乙车从B地返回C地的过程中，y（千米）与x（小时）之间的函数关系式（不需要写出自变量x的取值范围）；
3. （3）在乙车回到C地前，出发多少小时，两车之间的路程是15千米？请你直接写出答案．
答案解析收藏纠错 + 选题
23. (2021·富拉尔基模拟) 综合与实践：利用矩形的折叠开展数学活动，探究体会图形在轴对称，旋转等变换过程中的变化，及其蕴含的数学思想和方法．
动手操作：如图①，矩形纸片ABCD的边AB＝2 $\text{[math]}$ ，将矩形纸片ABCD对折，使点A与点D重合，点B与点C重合，折痕为EF ，然后展开，EF与AC交于点H；

如图②，将矩形ABCD沿过点A的直线折叠，使点B落在对角线AC上，且点B与点H重合，展开图形，折痕为AG ，连接GH；

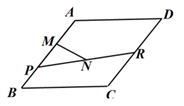
若在图①中连接BH ，得到如图③，点M是线段BH上的动点，点N是线段AH上的动点，连接AM ， MN ，且∠AMN＝∠ABH；

若在图②中连接BH ，交折痕AG于点Q ，隐去其它线段，得到如图④．
1. （1）解决问题：
  在图②中，∠ACB＝，BC＝， $\text{[math]}$ ＝，与△ABG相似的三角形有个；
2. （2）在图②中，AH²＝AE $\text{[math]}$ ▲ （从图②中选择一条线段填在空白处），并证明你的结论；
3. （3）在图③中，△ABH为三角形，设BM为x ，则NH＝（用含x的式子表示）；
4. （4）拓展延伸：
  在图④中，将△ABQ绕点B按顺时针方向旋转α（0°≤α≤180°），得到△A′BQ′，连接DQ′，则DQ′的最小值为，当tan∠CBQ′＝时，△DBQ′的面积最大值为．
答案解析收藏纠错 + 选题
24. (2021·富拉尔基模拟) 如图，已知抛物线y＝a $\text{[math]}$ ＋bx＋3（a≠0）与x轴交于点A（1，0）和点B（－3，0），与y轴交于点C．
1. （1）求抛物线解析式；
2. （2）若M是抛物线对称轴上的一点，则△ACM周长的最小值为；
3. （3）点N为第二象限抛物线上的动点，求△BCN面积的最大值及此时点N的坐标；
4. （4）点P是y轴上的一点，在坐标平面内存在点Q，使以A，C，P，Q为顶点的四边形是菱形，请直接写出点Q的坐标．
答案解析收藏纠错 + 选题