 C .
C .  D .
D . 
当 时,上式就是所有正整数的倒数的和
(*)
随着n的无限增加,(*)式中的第n项 将无限接近于0,那么(*)式的值会比10大吗?会比10000大吗?
自然的感觉是“聚沙成塔”、“积少成多”,即设法把很多小小的项累加起来变大.下面是实现这个想法的一种组合法:
用这种方法可以判定(*)式中:
“ 不是有理数”,对于这一事实的证明,最早出现在亚里士多德(Aristotle)的著作中,但他声明来源于毕达哥拉斯学派.欧几里得(Euclid)在《原本》中给出了证明.
证明:假设 应是有理数,由于
,所以必然有两个正整数a,b,
使 ,①
而且a,b互质(即没有1以外的公因数).
等式①两边平方,得
,即
.
所以 ▲ . ②
上面式子的右边是偶数,所以左边 也是偶数,因而b也是 ▲ ,
可设 (k是正整数),代入②,得
,
即 .
所以a也是偶数,这说明a,b都是偶数,不是 ▲ ,
与假设相矛盾,即 ▲ 有理数.

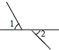
已知:如图, ,直线DE交AB于点G,
.

求证: .
证明:因为 ( ▲ ),
所以 ( ▲ ).
因为 (已知),
所以 ▲
(等量代换).
所以 ( ▲ ).