浙江省杭州市江干区2020-2021学年八年级下学期数学期末...

更新时间：2021-08-15 浏览次数：268 类型：期末考试

一、单选题

1. (2024八下·东阳期末) 下列垃圾分类标识中，是中心对称图形的是（　　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021八下·江干期末) 二次根式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八下·江干期末) 如果一个多边形的内角和等于540°，则它的边数为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
4. (2021八下·江干期末) 下列计算中正确的是（）

A . （﹣ $\text{[math]}$ ）²＝﹣3 B . $\text{[math]}$ ＝0.1 C . $\text{[math]}$ ＝1 $\text{[math]}$ D . 3 $\text{[math]}$ ＝ $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八下·江干期末) 反比例函数的图象经过（﹣1，3）点，则这个反比例函数的表达式为（）

A . y＝﹣ $\text{[math]}$ B . y＝ $\text{[math]}$ C . y＝﹣ $\text{[math]}$ D . y＝ $\text{[math]}$

答案解析收藏纠错 + 选题

6. (2021八下·江干期末) 某市四家工厂2019年和2020年的生产总值如表（单位：万元），则设这四家工厂2019年和2020年的平均生产总值分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ﹣ $\text{[math]}$ 的值为（）

单位	A厂	B厂	C厂	D厂
2019年	400	510	330	680
2020年	420	550	300	810

A . 40 B . 55 C . 160 D . 220

答案解析收藏纠错 + 选题

7. (2021八下·江干期末) 某公司计划用32m的材料沿墙（可利用）建造一个面积为120m²的仓库，设仓库中和墙平行的一边长为xm，则下列方程中正确的是（）

A . x（32﹣x）＝120 B . x（16﹣ $\text{[math]}$ x）＝120 C . x（32﹣2x）＝120 D . x（16﹣x）＝120

答案解析收藏纠错 + 选题
8. (2022八下·上城期中) 如图，四边形ABCD是菱形，点E、F分别在边BC、CD上，且BE＝DF，AB＝AE，若∠EAF＝75°，则∠C的度数为（）

A . 85° B . 90° C . 95° D . 105°

答案解析收藏纠错 + 选题
9. (2021八下·江干期末) 已知点A（x₁ ， y₁）在反比例函数y₁＝ $\text{[math]}$ 的图象上，点B（x₂ ， y₂）在一次函数y₂＝kx﹣k的图象上，当k＞0时，下列判断中正确的是（）

A . 当x₁＝x₂＞2时，y₁＞y₂ B . 当x₁＝x₂＜2时，y₁＞y₂ C . 当y₁＝y₂＞k时，x₁＜x₂ D . 当y₁＝y₂＜k时，x₁＞x₂

答案解析收藏纠错 + 选题
10. (2021八下·江干期末) 在一次活动课中，对如图所示的平行四边形（AD＞AB）进行折叠，第一次沿着AE折叠，点B落在点F处，接着两组同学分别尝试了两种不同的二次折叠，并给出了判断：组1：若沿着CF的中垂线折叠，则点D与点A必重合；组2：若沿着DF折叠，AD与DC所在的直线重合，且点A的对应点仍落在直线AF上，则 $\text{[math]}$ ＝ $\text{[math]}$ （）

A . 组1判断正确，组2判断正确 B . 组1判断正确，组2判断错误 C . 组1判断错误，组2判断正确 D . 组1判断错误，组2判断错误

答案解析收藏纠错 + 选题

二、填空题

11. (2021八下·江干期末) 平行四边形ABCD中，∠A＝40°，则∠D＝度

答案解析收藏纠错 + 选题
12. (2021八下·江干期末) 在一分钟跳绳测试中，甲、乙两班的平均成绩都为182个，方差S²_甲＝6.3，S²_乙＝5.5，成绩更为稳定的班级是.（填“甲”或“乙”）

答案解析收藏纠错 + 选题
13. (2021八下·江干期末) 如图，在矩形ABCD中，E，F分别是AB，AD的中点，若AC＝4，则EF的长是 .

答案解析收藏纠错 + 选题
14. (2021八下·江干期末) 若t是方程ax²+2x＝0（a≠0）的一个根，则 $\text{[math]}$ 的值为 .

答案解析收藏纠错 + 选题
15. (2021八下·江干期末) 定义菱形的两条对角线长之比为“对角线比”.
1. （1）若菱形成为正方形，则“对角线比”为；
2. （2）当“对角线比”为4，菱形面积为800时，菱形的边长为 .
答案解析收藏纠错 + 选题
16. (2022八下·杭州期末) 反比例函数y＝ $\text{[math]}$ ，当1≤x≤3时，函数y的最大值和最小值之差为4，则k＝.

答案解析收藏纠错 + 选题

三、解答题

17. (2021八下·江干期末) 计算：
1. （1） $\text{[math]}$ ﹣ $\text{[math]}$ ；
2. （2）（2 $\text{[math]}$ +3 $\text{[math]}$ ）².
答案解析收藏纠错 + 选题
18. (2021九上·武汉月考) 用指定的方法解方程：
1. （1）（x﹣4）²＝2（x﹣4）（因式分解法）；
2. （2） 2x²﹣4x﹣1＝0（公式法）.
答案解析收藏纠错 + 选题
19. (2021八下·江干期末) 如图，在▱ABCD中，∠BAD和∠BCD的平分线AF，CE分别与对角线BD交于点F，E.
求证：四边形AFCE是平行四边形.

答案解析收藏纠错 + 选题
20. (2021八下·江干期末) 某学校从九年级同学中任意选取20人进行“引体向上”体能测试，前后进行了两次测试，第一次测试绘制成统计图，第二次测试绘制成统计表.

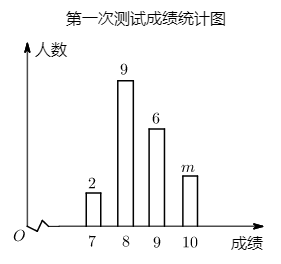
成绩

7

8

9

10

人数

1

5

10

4
1. （1） m＝，第一次测试成绩的中位数是，第二次测试成绩的众数是；
2. （2）请计算第一次测试的平均成绩；
3. （3）若9分及以上为优秀，请计算两次测试中优秀人数增加的百分比（精确到0.1%）.
答案解析收藏纠错 + 选题
21. (2021八下·江干期末) 已知：如图，在正方形ABCD中，BD为对角线，E、F分别是AD，CD上的点，且AE＝CF，连接BE、BF、EF.
1. （1）求证：EM＝FM；
2. （2）若DE：AE＝2：1，设S_△ABE＝S，求S_△BEF（用含S的代数式表示）.
答案解析收藏纠错 + 选题
22. (2021八下·江干期末) 阅读材料：
已知：一次函数y＝﹣x+b与反比例函数y＝ $\text{[math]}$ （x＞0），当两个函数的图象有交点时，求b的取值范围.
1. （1）方方给出了下列解答：
  ﹣x+b＝ $\text{[math]}$
  
  x²﹣bx+4＝0
  
  ∵两个函数有交点
  
  ∴△＝b²﹣16≥0
  
  但是方方遇到了困难：利用已学的知识无法解b²﹣16≥0这个不等式；
  
  此时，圆圆提供了另一种解题思路；
  
  第1步：先求出两个函数图象只有一个交点时，b＝ ▲ ；
  
  第2步：画出只有一个交点时两函数的图象（请帮圆圆在直角坐标系中画出图象）；
  
  第3步：通过平移y＝﹣x+b的图象，观察得出两个函数的图象有交点时b的取值范围是 ▲ .
  
  应用：
  
  如图，Rt△ABC中，∠C＝90°，BC的长为x，AC的长为y，且S_△ABC＝12.
2. （2）求y关于x的函数表达式；
3. （3）设x+y＝m，求m的取值范围.
答案解析收藏纠错 + 选题
23. (2021八下·江干期末) 如图，在矩形ABCD中，G为CD的中点，连接AG并延长交BC的延长线于点F，过G作EG⊥AF交直线BC于点E，连接AE.
1. （1）证明：∠DAG＝∠EAG；
2. （2）设 $\text{[math]}$ ＝k（k＞0）
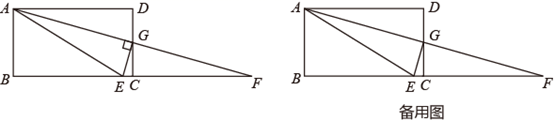
  ①若点E落在∠BAG的平分线上，求k的值.
  
  ②设m＝ $\text{[math]}$ ，求m关于k的函数表达式.
答案解析收藏纠错 + 选题