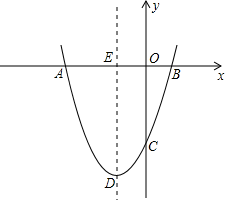
B .
B .  C .
C .  D .
D . 
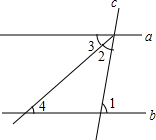

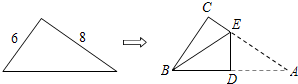
①AB=;②CD=(提示:过A作CD的垂线);③BC=.


参考数据:sin37°≈ ,cos37°≈
,tan37°≈
,sin22°≈
,cos22°≈
,tan22°≈
|
种类 |
A |
B |
C |
D |
E |
F |
|
上学方式 |
电动车 |
私家车 |
公共交通 |
自行车 |
步行 |
其他 |
并将调查结果绘制成如下不完整的统计图:

根据以上信息,回答下列问题:
解答几何问题常常需要添辅助线,其中平移图形是重要的添辅助线策略.
【问题情境】
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
小明在分析解题思路时想到了两种平移法:
方法1:平移线段FG使点F与点B重合,构造全等三角形;
方法2:平移线段BC使点B与点F重合,构造全等三角形;

【尝试应用】
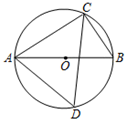
①求∠DMC的度数;
②连接AC交DE于点H,求 值.