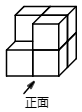
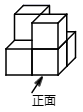
| 点 而点 由 得四边形 |
为保证小颖的推理更严谨,小明想在方框中“由 ,”和“得四边形……”之间作补充.应补充的是( )


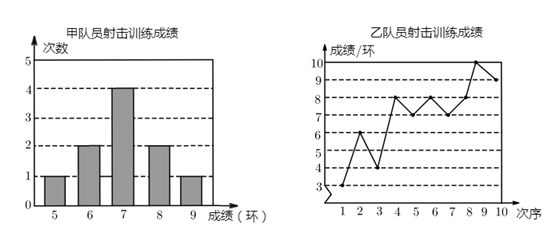 根据以上信息,整理分析数据如下表:
根据以上信息,整理分析数据如下表:
| 平均成绩(环) | 众数(环) | 方差 | |
| 甲 | | 7 | |
| 乙 | 7 | | 4.2 |
表格中 ,
,
的值分别是( )

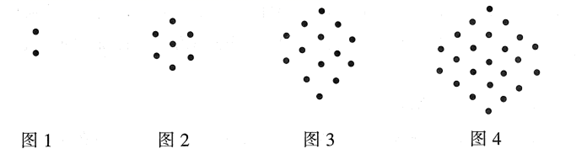
第一步
第二步
第三步
第四步
第五步
第六步
任务一 填空 在以上化简步骤中,其中有一步是根据分式的基本性质:“分式的分子与分母都乘(或除以)同一个不为零的整式,分式的值不变,”对分式进行通分.这是第 ▲ 步;
任务二 订正 请写出该分式化简的正确过程;
任务三 求值 当 时,求该分式的值.

已知:
求作: 的平分线
作法:⑴以点 为圆心,适当长为半径画弧,交
于点
,交
于点
;
⑵分别以点 ,
为圆心,大于
的长为半径画弧,两弧在
的内部相交于点
;
⑶画射线 ,射线
即为所求.
连接 ,
,请你根据上述作法,证明射线
为
的平分线.
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
你认为以上三个方案中,抽取的样本具有公平性的方案是哪一个?
|
样本容量 |
平均分 |
及格率 |
优秀率 |
最高分 |
最低分 |
|
100 |
93.5 |
| | 100 | 80 |
| 分数段统计(学生成绩记为 | |||||
| 分数段 | | | | | |
| 频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
![]()