B .
B .  C .
C . 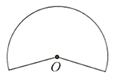 D .
D . 



①当n=3时,P,Q的跟随点的坐标为多少;
②写出P,Q的跟随点的坐标;(用含n的式子表示);
③记函数y=kx﹣1(﹣1≤x≤1,k≠0)的图象为图形G,若图形G上不存在P,Q的跟随点,求k的取值范围;
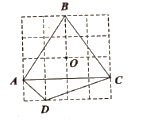
①在点P1( ,0),P2(
,
),P3(
,0)中,⊙O的关联点是.
②点P在直线y=﹣x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
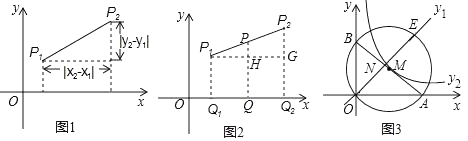
 图1
图1  图2
图2
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,