

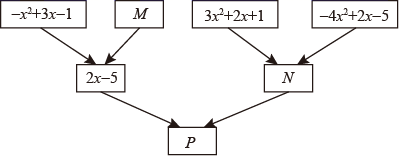
a.反映2020年中央财政脱贫专项资金分配额度的频数分布直方图如下(数据分成8组: ,
,
,
,
,
,
,
)
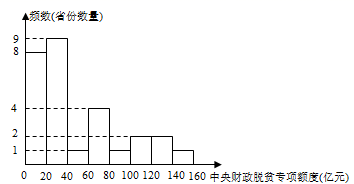
b.2020年中央财政脱贫专项资金在 这一组分配的额度是(亿元):
25;28;28;30;37;37;38;39;39
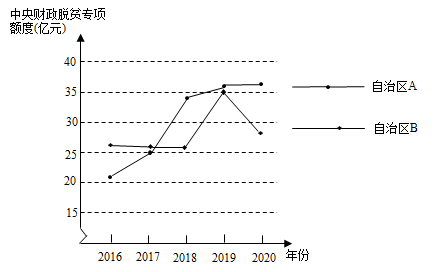
①比较2016年-2020年中央财政脱贫专项资金对自治区A,B的分配额度,方差 ▲ _
(填写“>”或者“<”);
②请结合统计数据,针对中央财政脱贫专项资金对自治区A,B脱贫攻坚工作的支持情况,说一说你的看法.
|
时间 | | |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
| 销量(斤) | | |
| 储存和损耗费用(元) | | |
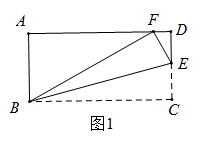
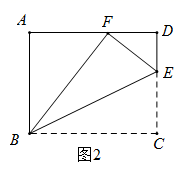
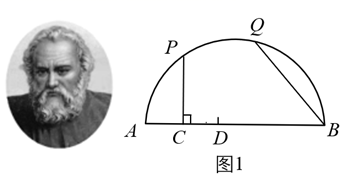
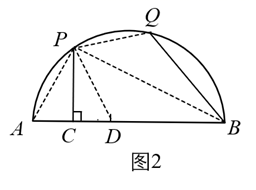
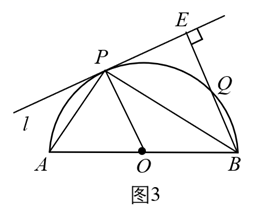
在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:如图1,点 是
上的任意一点,
于点
,点
在弦
上且
,在
上取一点
,使
,连接
,则有
.
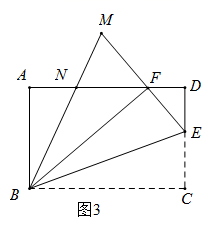
①当点 首次落在抛物线上,求
的值.
②当抛物线落在正方形内的部分,满足 随
的增大而减小时,请直接写出
的取值范围.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
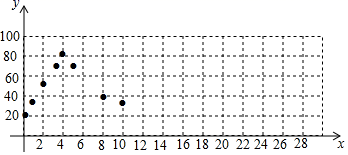
下面是小明的探究过程,请补充完整:
|
接通电源后的时间x(单位:min) |
0 |
1 |
2 |
3 |
4 |
5 |
8 |
10 |
16 |
18 |
20 |
21 |
24 |
32 |
… |
|
水箱中水的温度y(单位:℃) |
20 |
35 |
50 |
65 |
80 |
64 |
40 |
32 |
20 |
m |
80 |
64 |
40 |
20 |
… |
m的值为;
当4<x≤16时,写出一个符合表中数据的函数解析式 ▲ ;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象: