 B .
B .  C .
C .  D .
D . 




⑴在图中画出 以A为旋转中心,沿顺时针方向旋转
后的图形
;
⑵若点B的坐标为 ,点C的坐标为
,在图中建立直接坐标系,并画出
关于原点对称的图形
.
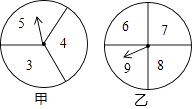
原题;如图①,点 分别在正方形
的边
上,
,连接
,则
,试说明理由,

∵ ,∴把
绕点A逆时针旋转
至
,可使
与
重合,∵
,∴
,即:点
共线,根据“
”,易证
, 得
;
如图②,四边形 中,
,点
分别在
上,
,若
都不是直角,则当
与
满足等量关系时,仍有
;
如图③,在 中,
,点
均在边
上,且
,猜想
应满足的等量关系,并写出推理过程.