河南省南阳市镇平县2020-2021学年九年级上学期数学期中...

更新时间：2021-10-28 浏览次数：108 类型：期中考试

一、单选题

1. (2023九上·内乡县月考) 下列二次根式中，是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·镇平期中) 一元二次方程x²﹣8x+20=0的根的情况是（　　）

A . 没有实数根 B . 有两个相等的实数根 C . 只有一个实数根 D . 有两个不相等的实数根

答案解析收藏纠错 + 选题
3. (2021九上·济南月考) 一个多边形的边长为2，3，4，5，6，另一个和它相似的多边形的最长边为24，则这个多边形的最短边长为（）

A . 6 B . 8 C . 12 D . 10

答案解析收藏纠错 + 选题
4. (2022九下·温州开学考) 用配方法解方程 $\text{[math]}$ ，变形结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·镇平期中) 如图，线段CD两个端点的坐标分别为C(4，4)，D(6，2)，以原点O为位似中心，在第一象限内将线段CD缩小为原来的一半后得到线段AB，则端点A的坐标为（）

A . (2，2) B . (3，3) C . (3，1) D . (4，1)

答案解析收藏纠错 + 选题
6. (2020九上·镇平期中) 近几年，手机支付用户规模增长迅速，据统计2016年手机支付用户约为4.69亿人，连续两年增长后，2018年手机支付用户达到约5.83亿人，如果设这两年手机支付用户的年均增长率为x，则根据题意可以列出方程为（）

A . 4.69（1+x）＝5.83 B . 4.69（1+2x）＝5.83 C . 4.69（1+x）²＝5.83 D . 4.69（1﹣x）²＝5.83

答案解析收藏纠错 + 选题
7. (2020九上·镇平期中) 已知，一个小球由桌面沿着斜坡向上前进了10cm，此时小球距离桌面的高度为5cm，则这个斜坡的坡度i为（）

A . 2 B . 1：2 C . 1： $\text{[math]}$ D . 1： $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·镇平期中) 比较大小错误的是（）

A . $\text{[math]}$ ＜ $\text{[math]}$ B . $\text{[math]}$ +2＜ $\text{[math]}$ ﹣1 C . $\text{[math]}$ ＞﹣6 D . $\text{[math]}$ ＞ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九上·镇平期中) 如图，在 $\text{[math]}$ 中，点D，E分别在 $\text{[math]}$ ， $\text{[math]}$ 上且 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$

A . 2：3 B . 4：9 C . 4：25 D . 4：19

答案解析收藏纠错 + 选题
10. (2020九上·镇平期中) 如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）

A . 等于 $\text{[math]}$ B . 等于 $\text{[math]}$ C . 等于 $\text{[math]}$ D . 随点E位置的变化而变化

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·镇平期中) 将方程2x²=1-3x化为一般形式是．

答案解析收藏纠错 + 选题
12. (2020九上·镇平期中) 比例尺为1∶4000000的地图上，两城市间的图上距离为3cm，则这两城市间的实际距离为km.

答案解析收藏纠错 + 选题
13. (2020九上·镇平期中) 满足﹣ $\text{[math]}$ ＜x＜ $\text{[math]}$ 的所有整数x的和是.

答案解析收藏纠错 + 选题
14. (2022·钦州模拟) 如图，河宽CD为100 $\text{[math]}$ 米，在C处测得对岸A点在C点南偏西30°方向、对岸B点在C点南偏东45°方向，则A、B两点间的距离是米.（结果保留根号）

答案解析收藏纠错 + 选题
15. (2023·宜阳模拟) 将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF.已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是.

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·镇平期中) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2020九上·镇平期中) 解下列方程；
1. （1） 4x²﹣121＝0；
2. （2） 2x（x﹣1）+6＝2（0.5x+3）；
3. （3） 4x²﹣8x﹣1＝0.
答案解析收藏纠错 + 选题
18. (2020九上·镇平期中) 如图，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD：AB＝3：1，CE垂直y轴于点E.
1. （1）求证： $\text{[math]}$ ；
2. （2）直接写出点B和点C的坐标.
答案解析收藏纠错 + 选题
19. (2020九上·镇平期中) 黄河，既是一条源远流长、波澜壮阔的自然河，又是一条孕育中华民族灿烂文明的母亲河，数学课外实践活动中，小林和同学们在黄河南岸小路上的A，B两点处，用测角仪分别对北岸的观景亭D进行测量.如图，测得∠DAC＝45°，∠DBC＝65°.若AB＝200米，求观景亭D到小路AC的距离约为多少米？（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

答案解析收藏纠错 + 选题
20. (2023九上·青神期中) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根.
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）当 $\text{[math]}$ 取满足条件的最大整数时，求方程的根.
答案解析收藏纠错 + 选题
21. (2020九上·镇平期中)
1. （1）问题情境：如图1，Rt $\text{[math]}$ 中，∠ACB＝90°，CD⊥AB，我们可以利用 $\text{[math]}$ 与 $\text{[math]}$ 相似证明AC²＝AD•AB，这个结论我们称之为射影定理，试证明这个定理.
2. （2）结论运用：如图2，正方形ABCD的边长为6，点O是对角线AC，BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF，试利用射影定理证明 $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2022·淮南模拟) 位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一．某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度．如图所示，他们在地面一条水平步道MP上架设测角仪，先在点M处测得观星台最高点A的仰角为22°，然后沿MP方向前进16m到达点N处，测得点A的仰角为45°．测角仪的高度为1.6m求观星台最高点A距离地面的高度（结果精确到0.1m．参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40， $\text{[math]}$ ≈1.41）．

答案解析收藏纠错 + 选题
23. (2020九上·镇平期中) 如图1，在Rt $\text{[math]}$ 中，∠B＝90°，AB＝4，BC＝2，点D，E分别是边BC，AC的中点，连接DE.将 $\text{[math]}$ 绕点C逆时针方向旋转，记旋转角为α.
1. （1）问题发现
  ①当α＝0°时， $\text{[math]}$ ＝；
  
  ②当α＝180°时， $\text{[math]}$ ＝；
2. （2）拓展探究
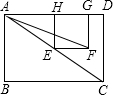
  试判断当0°＜α＜360°时， $\text{[math]}$ 的大小有无变化？请仅就图2的情形给出证明；
3. （3）问题解决
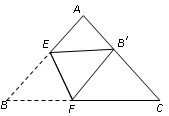
  当 $\text{[math]}$ 绕点C逆时针旋转至A，B，E三点在同一条直线上时，求线段BD的长.
答案解析收藏纠错 + 选题