初中数学浙教版九年级上册专题复习：用频率估计概率

更新时间：2021-10-15 浏览次数：106 类型：复习试卷

一、单选题

1. (2021·张店模拟) 某小组在“用频率估计概率”的试验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的试验最有可能的是（）

A . 从一副扑克牌中任意抽取一张，这张牌是“红色的” B . 掷一枚质地均匀的硬币，落地时结果是“正面朝上” C . 在装有1个红球和2个白球（除颜色外完全相同）的不透明袋子里随机摸出一个球是“白球” D . 掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6

答案解析收藏纠错 + 选题
2. (2021九上·茂名月考) 在一个不透明的袋子里装有红球，黄球共60个，这些球除颜色外其他都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（）

A . 9 B . 15 C . 18 D . 24

答案解析收藏纠错 + 选题

3. (2024·宁明模拟) 某射击运动员在同一条件下的射击成绩记录如下：

射击次数	20	80	100	200	400	1000
“射中九环以上”的次数	18	68	82	168	327	823
“射中九环以上”的频率（结果保留两位小数）	0.90	0.85	0.82	0.84	0.82	0.82

根据频率的稳定性，估计这名运动员射击一次时“射中九环以上”的概率约是（）

A . 0.90 B . 0.82 C . 0.85 D . 0.84

答案解析收藏纠错 + 选题

4. (2021八下·滦南期末) 嘉琪在做“抛一枚正六面体骰子”的实验时，他连续抛了10次，其中“6”点向上共出现3次，则出现“6”点向上的频率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

5. (2021七下·郓城期末) 绿豆在相同条件下的发芽试验，结果如下表格

每批粒数n	100	300	400	600	1000	2000	3000
发芽的粒数m	96	282	382	570	948	1904	2850
发芽频率（m/n）	0.960	0.940	0.955	0.950	0.948	0.952	0.950

①当n＝400时，绿豆发芽的频率为0.955，所以绿豆发芽的概率是0.955；②根据上表，估计绿豆发芽的概率是0.95；③若n为4000，估计绿豆发芽的粒数为3800．其中推断合理的是（）

A . ① B . ①② C . ①②③ D . ②③

答案解析收藏纠错 + 选题

6. (2020九上·光明期末) 小明在一次用“频率估计概率”的实验中，把对联“海水朝朝朝朝朝朝朝落，浮云长长长长长长长消”中的每个汉字分别写在同一种卡片上，然后把卡片无字的面朝上，随机抽取一张，并统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的实验最有可能是（）

A . 抽出的是“朝”字 B . 抽出的是“长”字 C . 抽出的是独体字 D . 抽出的是带“氵”的字

答案解析收藏纠错 + 选题
7. (2023九上·坪山月考) 一个密闭不透明的盒子里有若干个白球，在不许将球倒出来数的情况下，为了估计白球数，小刚向其中放入了8个黑球，搅匀后从中随意摸出一个球记下颜色，再把它放回盒中，不断重复这一过程，共摸球400次，其中80次摸到黑球，你估计盒中大约有白球（）

A . 32个 B . 36个 C . 40个 D . 42个

答案解析收藏纠错 + 选题

8. (2020九上·孝义期末) 历史上，数学家们曾做过好多次抛掷硬币的试验，其中一些试验结果如下表所示：

实验者	抛掷次数 $\text{[math]}$	“正面向上”的次数 $\text{[math]}$	“正面向上”的频率 $\text{[math]}$
棣莫弗	2048	1061	0.5181
布丰	4040	2048	0.5069
费勒	10000	4979	0.4979
皮尔逊	12000	6019	0.5016
皮尔逊	24000	12012	0.5005

则关于抛掷硬币的试验，下列说法正确的是（）

A . 随着抛掷次数的增加，频率在0.5附近摆动的幅度越来越小 B . 随着抛掷次数的增加，频率等于0.5 C . 每多抛一次，频率会更加接近0.5 D . 无论抛掷多少次，频率与概率都不可能相等

答案解析收藏纠错 + 选题

9. (2020九上·绍兴月考) 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（　　）

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

A . 一副去掉大小王的普迺扑克牌洗匀后，从中任抽一张牌的花色是红桃 B . 从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率 C . 抛一枚硬币，出现正面的概率 D . 抛一个质地均匀的正六面体骰子（六个面上分别标有1，2，3，4，5，6），向上的面点数是5

答案解析收藏纠错 + 选题

10. (2021九上·郫都期末) 在利用正六面体骰子进行频率估计概率的实验中，小颖同学统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（）

A . 朝上的点数是 5 的概率 B . 朝上的点数是奇数的概率 C . 朝上的点数是大于 2 的概率 D . 朝上的点数是 3 的倍数的概率

答案解析收藏纠错 + 选题

二、填空题

11. (2021八下·南京期中) 综合实践小组的同学们在相同条件下做了测定某种黄豆种子发芽率的实验，结果如表所示：

黄豆种子数（单位：粒）	800	1000	1200	1400	1600	1800	2000
发芽种子数（单位：粒）	762	948	1142	1331	1518	1710	1902
种子发芽的频率（结果保留至小数点后三位）	0.953	0.948	0.952	0.951	0.949	0.950	0.951

那么这种黄豆种子发芽的概率约为（精确到0.01）.

答案解析收藏纠错 + 选题

12. (2021九上·临海期末) 某林业部门要考察某种幼树在一定条件下的移植成活率，在同样的条件下对这种幼树进行大量移植，并统计成活情况，记录如下:

移植总数（n）	50	200	1000	5000	10000
成活（m）	46	171	912	4480	9020
成活的频率（ $\text{[math]}$ ）	0.920	0.855	0.912	0.896	0.902

由此可以估计幼树移植成活的概率为（结果保留小数点后一位）

答案解析收藏纠错 + 选题

13. (2024九上·乌鲁木齐期末) 某商场设立了一个可以自由转动的转盘，并规定：顾客购物30元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：

转动转盘的次数	100	200	300	500	1000
落在“签字笔”区域的次数	65	122	190	306	601

假如你去转动该转盘一次.你获得签字笔的概率约是.（精确到0.1）

答案解析收藏纠错 + 选题

14. (2021八下·盐城期末) 某数学社团做摸球试验：一只不透明的袋子中装有若干个红球和白球，这些球除颜色外都相同.将这个袋中的球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得如下数据：

摸球的个数n	200	300	400	500	1000	1600	2000
摸到白球的个数m	116	192	232	298	590	968	1202
摸到白球的频率 $\text{[math]}$	0.580	0.640	0.580	0.596	0.590	0.605	0.601

根据以上数据估计，摸到白球的概率约为（精确到0.01）.

答案解析收藏纠错 + 选题

15. (2021·鄞州模拟) 对一批口罩进行抽检，统计合格口罩的只数，得到合格口罩的频率如下：

抽取只数（只）	50	100	150	500	1000	2000	10000	50000
合格频率	0.82	0.83	0.82	0.83	0.84	0.84	0.84	0.84

估计从该批次口罩中任抽一只口罩是合格品的概率为.

答案解析收藏纠错 + 选题

16. (2021九上·大洼期末) 一名篮球运动员在某段时间内进行定点投篮训练，其成绩如下表：

投篮次数

10

100

10 000

投中次数

9

89

9012

试估计这名运动员在这段时间内定点投篮投中的概率是 .

答案解析收藏纠错 + 选题

17. (2021九上·锦州期末) 某批足球的质量检验结果如下：

抽取的足球数n	100	200	400	600	800	1000	1200
优等品频数m	93	192	380	561	752	941	1128
优等品频率 $\text{[math]}$	0.930	0.960	0.950	0.935	0.940	0.941	0.940

从这批足球中，任意抽取的一只足球是优等品的概率的估计值是.

答案解析收藏纠错 + 选题

三、解答题

18. (2024九上·龙川期末) 第一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定在0.4，估计袋中红球的个数.

答案解析收藏纠错 + 选题
19. 某人承包了一池塘养鱼，他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼，把每条鱼都作上标记，放回鱼塘；过了2天，他让他父亲从鱼塘内打捞上了50条鱼，结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤，平均每条鱼估计2.3斤，你能帮助他估计一下今年的收入情况吗?

答案解析收藏纠错 + 选题
20. 对某厂生产的直径为4cm的乒乓球进行产品质量检查，结果如下：
1. （1）计算各次检查中“优等品”的频率，填入表中；
  抽取球数n 50 100 500 1000 5000
  优等品数m 45 92 455 890 4500
  优等品频率 $\text{[math]}$
2. （2）该厂生产乒乓球优等品的概率约为多少?
答案解析收藏纠错 + 选题
21. 下面给大家介绍密码破译的知识：
密码破译本质上是一个寻找偶然事情规律的一种游戏．为了简明，我们以英语例子加以说明．
如果要传递的消息是用英语写的，你可以随意地用两个数字来代替英语中的一个字母，比如为叙述方便，用00，01，02，…25来代替26个英文字母，而每个单词之间用26隔开．当接到这样编排密码时首先要对所有的数码在密码中出现的次数进行统计，算出每个数码出现的频率．再逐步分析出每个数码代表的是哪个字母，弄清了这个问题，密码也就能破译出来了．假如你收到的密码中有一段是：
070015152426130422262404001726191426241420
你能破译出这段密码吗？

答案解析收藏纠错 + 选题
22. 某批乒乓球的质量检验结果如下：
抽取的乒乓球数n
200
500
1000
1500
2000
优等品频数m
188
471
946
1426
1898
优等品频率 $\text{[math]}$
0.940
0.942
0.946
0.951
0.949
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于 $\text{[math]}$ ，问至少取出了多少个黑球？

答案解析收藏纠错 + 选题
23.
某商场“五一”期间为进行有奖销售活动，设立了一个可以自由转动的转盘．商场规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
转动转盘的次数n
100
200
400
500
800
1000
落在“可乐”区域的次数m
60
122
240
298

604
落在“可乐”区域的频率 $\text{[math]}$
0.6
0.61
0.6

0.59
0.604
（1）完成上述表格；（结果全部精确到0.1）
（2）请估计当n很大时，频率将会接近　？，假如你去转动该转盘一次，你获得“可乐”的概率约是　？　；（结果全部精确到0.1）
（3）转盘中，表示“洗衣粉”区域的扇形的圆心角约是多少度？

答案解析收藏纠错 + 选题
24. 小颖和小红两位同学在做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
（1）计算“3点朝上”的频率和“5点朝上”的频率．
（2）小颖说：“根据实验得出，出现5点朝上的机会最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次．”小颖和小红的说法正确吗？为什么？

答案解析收藏纠错 + 选题
25.
小明在操场上做游戏，他发现地上有一个不规则的封闭图形ABC．为了知道它的面积，小明在封闭图形内划出了一个半径为1米的圆，在不远处向圈内掷石子，且记录如下：
求出封闭图形ABC的面积．
掷石子次数石子落在的区域
50次
150次
300次
石子落在⊙O内（含⊙O上）的次数m
14
43
93
石子落在阴影内的次数n
19
85
186

答案解析收藏纠错 + 选题
26. 在4件同型号的产品中，有1件不合格品和3件合格品．
（1）从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
（2）在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，通过大量重复这种试验后发现，抽到合格品的频率稳定在0.9，则可以推算出x的值大约是多少？

答案解析收藏纠错 + 选题
27.
一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
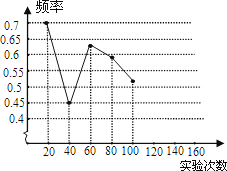
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52

78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56

（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？

答案解析收藏纠错 + 选题
28. 王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
2
5
6
4
10
3
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

初中数学浙教版九年级上册专题复习：用频率估计概率

副标题：

*注意事项：

初中数学浙教版九年级上册专题复习：用频率估计概率

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

抽取球数n	50	100	500	1000	5000
优等品数m	45	92	455	890	4500
优等品频率 $\text{[math]}$

抽取的乒乓球数n	200	500	1000	1500	2000
优等品频数m	188	471	946	1426	1898
优等品频率 $\text{[math]}$	0.940	0.942	0.946	0.951	0.949

转动转盘的次数n	100	200	400	500	800	1000
落在“可乐”区域的次数m	60	122	240	298		604
落在“可乐”区域的频率 $\text{[math]}$	0.6	0.61	0.6		0.59	0.604

掷石子次数石子落在的区域	50次	150次	300次
石子落在⊙O内（含⊙O上）的次数m	14	43	93
石子落在阴影内的次数n	19	85	186

实验次数	20	40	60	80	100	120	140	160
“車”字朝上的频数	14	18	38	47	52		78	88
相应的频率	0.7	0.45	0.63	0.59	0.52	0.55	0.56

投篮次数	10	100	10 000
投中次数	9	89	9012

朝上的点数	1	2	3	4	5	6
出现的次数	7	9	6	8	20	10

朝上的点数	1	2	3	4	5	6
出现的次数	2	5	6	4	10	3