山西省吕梁市孝义市2020-2021学年九年级上学期数学期末...

更新时间：2024-07-13 浏览次数：232 类型：期末考试

一、单选题

1. (2024九上·东阳开学考) 推进生态文明建设，实行垃圾分类和资源化利用是每个公民义不容辞的责任．下列四幅图是垃圾分类标志图案，每幅图案下配有文字说明．则四幅图案中既是轴对称图形，又是中心对称图形的是（）

A . 有害垃圾 B . 可回收物 C . 厨余垃圾 D . 其他垃圾

答案解析收藏纠错 + 选题
2. (2020九上·孝义期末) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的根的情况，下列说法正确的是（）

A . 有一个实数根 B . 有两个不相等的实数根 C . 有两个相等的实数根 D . 没有实数根

答案解析收藏纠错 + 选题
3. (2020九上·孝义期末) 如图是用卡钳测量容器内径的示意图，已知卡钳的四个端点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 到支点 $\text{[math]}$ 的距离满足 $\text{[math]}$ ，且 $\text{[math]}$ ．现在只要测得卡钳外端 $\text{[math]}$ ， $\text{[math]}$ 两个端点之间的距离，就可以计算出容器的内径 $\text{[math]}$ 的大小。这种测量原理用到了（）

A . 图形的旋转 B . 图形的平移 C . 图形的轴对称 D . 图形的相似

答案解析收藏纠错 + 选题

4. (2020九上·孝义期末) 历史上，数学家们曾做过好多次抛掷硬币的试验，其中一些试验结果如下表所示：

实验者	抛掷次数 $\text{[math]}$	“正面向上”的次数 $\text{[math]}$	“正面向上”的频率 $\text{[math]}$
棣莫弗	2048	1061	0.5181
布丰	4040	2048	0.5069
费勒	10000	4979	0.4979
皮尔逊	12000	6019	0.5016
皮尔逊	24000	12012	0.5005

则关于抛掷硬币的试验，下列说法正确的是（）

A . 随着抛掷次数的增加，频率在0.5附近摆动的幅度越来越小 B . 随着抛掷次数的增加，频率等于0.5 C . 每多抛一次，频率会更加接近0.5 D . 无论抛掷多少次，频率与概率都不可能相等

答案解析收藏纠错 + 选题

5. (2020九上·孝义期末) 如果反比例函数 $\text{[math]}$ 的图象在第一、三象限内，则下列说法正确的是（）

A . $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小 B . $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大 C . $\text{[math]}$ 的取值范围为 $\text{[math]}$ D . $\text{[math]}$ 的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·西丰月考) 将抛物线 $\text{[math]}$ 的向右平移1个单位长度，再向下平移3个单位长度后，得到抛物线的解析式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·孝义期末) 如图， $\text{[math]}$ 和 $\text{[math]}$ 是位似图形，点 $\text{[math]}$ 是位似中心，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点．若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，周长为 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的面积为 $\text{[math]}$ B . $\text{[math]}$ 的面积为 $\text{[math]}$ C . $\text{[math]}$ 的周长为 $\text{[math]}$ D . $\text{[math]}$ 的周长为 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·孝义期末) 已知二次函数 $\text{[math]}$ ，下列说法正确的是（）

A . 该函数的最小值为2 B . 该函数的最小值为1 C . 该函数的最大值为2 D . 该函数的最大值为1

答案解析收藏纠错 + 选题
9. (2020九上·孝义期末) 近似眼镜的度数 $\text{[math]}$ （度）与镜片焦距 $\text{[math]}$ （米）之间具有如图所示的反比例函数关系，若要配制一副度数小于400度的近似眼镜，则镜片焦距 $\text{[math]}$ 的取值范围是（）

A . 0米 $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . 0米 $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
10. (2020九上·孝义期末) 如图， $\text{[math]}$ 为半圆 $\text{[math]}$ 的直径，半径 $\text{[math]}$ ．以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021·吉林模拟) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
12. (2020九上·孝义期末) 数学课上，老师提出如下问题：“如图，用一段长为 $\text{[math]}$ 的篱笆围成一个一边靠墙的矩形菜园（墙足够长）．这个矩形的长、宽各为多少时，菜园的面积最大？”小慧设菜园的面积为 $\text{[math]}$ ，菜园的…为xm，列出 $\text{[math]}$ ．则自变量x的实际意义是．

答案解析收藏纠错 + 选题
13. (2020九上·孝义期末) 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，顶点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，顶点 $\text{[math]}$ 和 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，且对角线 $\text{[math]}$ 轴，则 $\text{[math]}$ 的面积等于．

答案解析收藏纠错 + 选题
14. (2021九上·南雄月考) 已知函数 $\text{[math]}$ 图像上两点 $\text{[math]}$ ，其中 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填大于小于或等于）．

答案解析收藏纠错 + 选题
15. (2020九上·孝义期末) 如图所示，复印纸的型号有A₀ ， A₁ ， A₂ ， A₃ ， A₄等，它们之间存在着这样一种关系：将其中某一型号（如A₃）的复印纸沿较长边的中点对折，就能得到两张下一型号（A₄）的复印纸，且得到的两个矩形都和原来的矩形相似，那么这些型号的复印纸的长、宽之比为．

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·孝义期末)
1. （1）解方程： $\text{[math]}$
2. （2）解方程： $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2020九上·孝义期末) 如图，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）交于点 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求出点 $\text{[math]}$ 的坐标及反比例函数的关系表达式；
2. （2）请直接写出不等式 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
18. (2020九上·孝义期末) 如图是一个能自由转动的正五边形转盘，这个转盘被五条分割线分成形状相同，面积相等的五部分，且每个部分分别标有1、2、3、4、5五个数字，指针的位置固定不动，让转盘自由转动，当转盘停止后，记录指针指向的数（当指针指向分割线时，视其指向分割线左边的区域）．
1. （1）若转动该转盘一次，则指针指向的数字为偶数的概率为；
2. （2）若连续转动转盘两次，请用“列表法”或“画树状图法”，求出两次指针指向的数字和为偶数的概率．
答案解析收藏纠错 + 选题
19. (2020九上·孝义期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径的圆与 $\text{[math]}$ 交于点 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 相切，并且交 $\text{[math]}$ 于点 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2020九上·孝义期末) 阅读下列材料，并完成相应的学习任务：
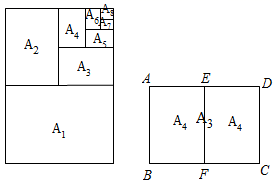
图形旋转的应用．图形的旋转是全等变换（平移、轴对称、旋转）中重要的变换之一，利用图形旋转中的对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变等性质，可以将一般图形转化成特殊图形，从而达到解决问题的目的．

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ．过点 $\text{[math]}$ 作互相垂直的两条直线，即 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．

分析：将 $\text{[math]}$ 以点 $\text{[math]}$ 为旋转中心顺时针旋转，使得旋转后 $\text{[math]}$ 的对应线段所在直线垂直于 $\text{[math]}$ ，并且交 $\text{[math]}$ 于点 $\text{[math]}$ ，旋转后 $\text{[math]}$ 的对应线段所在直线交 $\text{[math]}$ 于点 $\text{[math]}$ ．则容易证明四边形 $\text{[math]}$ 为正方形．因为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ ，

所以 $\text{[math]}$ ．

学习任务：
1. （1）四边形 $\text{[math]}$ 的面积等于；
2. （2）如图，在 $\text{[math]}$ 中， $\text{[math]}$ ：
  ①作出 $\text{[math]}$ 的外接圆 $\text{[math]}$ ；
  
  ②作 $\text{[math]}$ 的平分线，与 $\text{[math]}$ 交于点 $\text{[math]}$ ．
  
  要求：尺规作图，不写作法，但保留作图痕迹
3. （3）在（2）的基础上，若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积等于．
答案解析收藏纠错 + 选题
21. (2023九上·小店月考) 2020年秋冬以来，由于全国大葱种植面积的减少与产量的减产，10月份到12月份，大葱的批发价格持续走高。10月份大葱的批发价格为5元/公斤，12月份大葱的批发价格涨到7.2元/公斤．
1. （1）求10月份到12月份大葱批发价格的月平均增长率；
2. （2）进入12月份以来，某农贸市场按照7.2元/公斤的批发价购进大葱进行销售，销售价格为10元/公斤，每天能销售大葱500公斤，为了扩大销售，增加盈利，最大限度让利于顾客，该农贸市场决定对大葱进行降价销售，根据市场调查发现，大葱的销售单价每降低0.1元，每天的销售量将增加40公斤，求当大葱的销售价格降低多少元时，该农贸市场每天销售大葱的利润为1640元？
答案解析收藏纠错 + 选题
22. (2020九上·孝义期末) 综合与实践
已知四边形 $\text{[math]}$ 与 $\text{[math]}$ 均为正方形．
1. （1）数学思考：
  如图1，当点 $\text{[math]}$ 在 $\text{[math]}$ 边上，点 $\text{[math]}$ 在 $\text{[math]}$ 边上时，线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是，位置关系是．
2. （2）在图1的基础上，将正方形 $\text{[math]}$ 以点 $\text{[math]}$ 为旋转中心，逆时针旋转角度 $\text{[math]}$ ，得到图2，则（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；
  拓展探索：
3. （3）如图3，若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，且 $\text{[math]}$ ，则线段 $\text{[math]}$ 长为．（直接写出答案即可，不要求写过程）．
答案解析收藏纠错 + 选题
23. (2021·日喀则模拟) 综合与探究
如图，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ 两点，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．点 $\text{[math]}$ 是直线 $\text{[math]}$ 上方抛物线上的一个动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，垂足为 $\text{[math]}$ ，并且交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）请直接写出抛物线与直线 $\text{[math]}$ 的函数关系表达式；
2. （2）当 $\text{[math]}$ 时，求出点 $\text{[math]}$ 的坐标；
3. （3）是否存在点 $\text{[math]}$ ， $\text{[math]}$ ？若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题