安徽省安庆市外国语学校2021-2022学年九年级上学期数学...

更新时间：2024-07-31 浏览次数：127 类型：月考试卷

一、单选题

1. (2021九上·安庆月考) 下列函数中属于二次函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·安庆月考) 抛物线y＝2（x﹣1）²+5的顶点坐标是（）

A . （1，5） B . （2，1） C . （2，5） D . （﹣1，5）

答案解析收藏纠错 + 选题
3. (2021九上·安庆月考) 下列函数中，y随x的增大而减小的是（）

A . y＝x+1 B . y＝2x²（x＞0） C . y＝﹣x²（x＜0） D . y＝﹣x²（x＞0）

答案解析收藏纠错 + 选题
4. (2021九上·安庆月考) 对于二次函数y=-2(x+3) $\text{[math]}$ 的图象，下列说法错误的是（）

A . 开口向下 B . 对称轴是直线x=-3 C . 顶点坐标为(-3，0) D . 当x<-3时，y随x的增大而减小

答案解析收藏纠错 + 选题
5. (2021九上·安庆月考) 二次函数y=x²+bx+c的图象上有两点（3，4）和（﹣5，4），则此拋物线的对称轴是直线（）

A . x=﹣1 B . x=1 C . x=2 D . x=3

答案解析收藏纠错 + 选题
6. (2024九上·东莞期中) 将二次函数 $\text{[math]}$ 的图象向右平移2个单位，再向下平移3个单位，得到的函数图象的表达式是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·景县期末) 已知点A（3，y₁），B（4，y₂），C（﹣3，y₃）均在抛物线y＝2x²﹣4x+m上，下列说法中正确的是（）

A . y₃＜y₂＜y₁ B . y₂＜y₁＜y₃ C . y₃＜y₁＜y₂ D . y₁＜y₂＜y₃

答案解析收藏纠错 + 选题

8. (2021九上·安庆月考) 根据表中的二次函数y=ax²+bx+c的自变量x与函数y的对应值，可判断该二次函数的图象与x轴（）

x	…	﹣1	0	1	2	…
y	…	4	﹣0.5	﹣2	﹣0.5	…

A . 只有一个交点 B . 有两个交点，且它们分别在y轴两侧 C . 有两个交点，且它们均在y轴同侧 D . 无交点

答案解析收藏纠错 + 选题

9. (2021九上·安庆月考) 在同一平面直角坐标系中，函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2024·新疆维吾尔自治区模拟) 已知二次函数 $\text{[math]}$ 的图象如图所示，有下列5个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ （ $\text{[math]}$ ）；⑤若方程 $\text{[math]}$ ＝1有四个根，则这四个根的和为2，其中正确的结论有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·安庆月考) 写出一个对称轴是y轴的抛物线的解析式：．

答案解析收藏纠错 + 选题
12. (2021九上·安庆月考) 二次函数y＝2x²﹣4x+1的最小值是．

答案解析收藏纠错 + 选题
13. (2021九上·安庆月考) 已知二次函数y＝﹣x²＋bx＋c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是．

答案解析收藏纠错 + 选题
14. (2021九上·安庆月考) 已知抛物线y＝x²＋2x﹣3的图象与x轴交于A，B两点，在抛物线上存在一点P，使△ABP的面积为10，则点P的坐标为．

答案解析收藏纠错 + 选题

三、解答题

15. (2021九上·温州月考) 已知抛物线的解析式为y＝﹣3x²+6x+9．
1. （1）求此抛物线的对称轴；
2. （2）直接写出抛物线与x坐标轴的交点坐标．
答案解析收藏纠错 + 选题
16. (2021九上·安庆月考) 已知抛物线与 $\text{[math]}$ 交于A（－1，0）、B（3，0）两点，与 $\text{[math]}$ 轴交于点C（0，3），求抛物线的解析式；

答案解析收藏纠错 + 选题
17. (2021九上·安庆月考) 把抛物线y＝ax²+bx+c向左平移2个单位，同时向下平移1个单位后，恰好与抛物线y＝2x²+4x+1重合，请求出a、b、c的值．

答案解析收藏纠错 + 选题
18. (2021九上·安庆月考) 如图，A（﹣1，0）、B（2，﹣3）两点在一次函数y₁＝﹣x+m与二次函数y₂＝ax²+bx﹣3的图象上．
1. （1）求m的值和二次函数的解析式；
2. （2）请直接写出使y₁≤y₂时自变量x的取值范围．
答案解析收藏纠错 + 选题
19. (2022·路北模拟) 2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为 $\text{[math]}$ 轴，过跳台终点 $\text{[math]}$ 作水平线的垂线为 $\text{[math]}$ 轴，建立平面直角坐标系.图中的抛物线 $\text{[math]}$ 近似表示滑雪场地上的一座小山坡，某运动员从点 $\text{[math]}$ 正上方 $\text{[math]}$ 米处的 $\text{[math]}$ 点滑出，滑出后沿一段抛物线 $\text{[math]}$ 运动.
1. （1）当运动员运动到离 $\text{[math]}$ 处的水平距离为4米时，离水平线的高度为8米，求抛物线 $\text{[math]}$ 的函数解析式（不要求写出自变量 $\text{[math]}$ 的取值范围）；
2. （2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为1米？
3. （3）当运动员运动到坡顶正上方，且与坡顶距离超过3米时，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
20. (2021九上·安庆月考) 我们知道，二次函数y＝a（x﹣h）²+k（a≠0）的图象是一条抛物线，现定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将抛物线y′向上平移m（m＞0）个单位，得到新的抛物线y_m ，我们称y_m叫做二次函数y＝a（x﹣h）²+k（a≠0）的m阶变换．
1. （1）已知：二次函数y＝2（x+2）²+1，它的顶点关于原点的对称点为，这个抛物线的2阶变换的表达式为．
2. （2）若二次函数M的6阶变换的关系式为y₆＝（x﹣1）²+5．
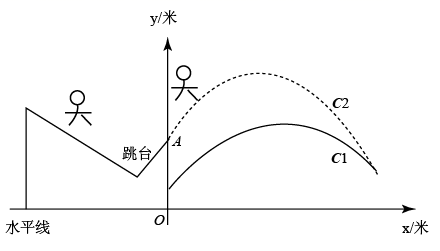
  ①二次函数M的函数表达式为 ▲ ．
  
  ②若二次函数M的顶点为点A，与x轴相交的两个交点中左侧交点为点B，动点P在抛物线y₆上，作PD⊥直线AB，请求出PD最小时P点的坐标．
答案解析收藏纠错 + 选题