初中数学浙教版八年级上册专题复习：勾股定理

更新时间：2021-11-02 浏览次数：170 类型：复习试卷

一、单选题

1. (2021九上·哈尔滨月考) 已知一个直角三角形的两直角边长分别为5和12，则第三边长是（）

A . 13 B . 14 C . 15 D . 16

答案解析收藏纠错 + 选题
2. (2024八上·武侯月考) 在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若a²＝b²+c² ，则（　　）

A . ∠A＝90° B . ∠B＝90° C . ∠C＝90° D . ∠C＝∠A+∠B

答案解析收藏纠错 + 选题
3. (2021八上·滕州月考) 下列各组数中，是勾股数的是（）

A . 0.3，0.4，0.5 B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . 16，63，65 D . 5，12，14

答案解析收藏纠错 + 选题
4. (2021九上·南山月考) 如图，正方形 ABCD的边长为2，点E从点A出发沿着线段AD向点D运动(不与点A，D重合)，同时点F从点D出发沿着线段DC向点C运动(不与点D，C重合，点E与点F的运动速度相同．BE与AF相交于点G，H为BF中点、则有下列结论：
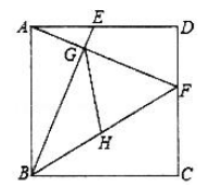
①∠BGF是定值；②FB平分∠AFC：③当E运动到AD中点时，GH= $\text{[math]}$ ：④当AG+BG= $\text{[math]}$ 时，四边形GEDF的面积是 $\text{[math]}$ ，其中正确的是（ )

A . ①②④ B . ①②③ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
5. (2023·海丰模拟) 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则 AE的长为（）

A . 10 B . 8 C . 6 D . 4

答案解析收藏纠错 + 选题
6. (2021九上·尧都期末) 把边长为3的正方形 $\text{[math]}$ 绕点A顺时针旋转45°得到正方形 $\text{[math]}$ ，边 $\text{[math]}$ 与 $\text{[math]}$ 交于点O，则四边形 $\text{[math]}$ 的周长是（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八上·余杭月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 沿DE翻折，使点A与点B重合，则CE的长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八上·滕州月考) 直角三角形的直角边长分别为3，4，则直角三角形的周长为（）

A . 5 B . 12 C . 12或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图所示，正方形网格中的△ABC，若小方格边长为1，则△ABC是（）

A . 直角三角形 B . 锐角三角形 C . 钝角三角形 D . 以上答案都不对

答案解析收藏纠错 + 选题
10. 如图，圆柱的高BC为20cm，底面周长是32 cm，一只蚂蚁从点A爬到点P处吃食，且PC= $\text{[math]}$ BC，则最短路线长为（）

A . 20 cm B . 13 cm C . 14 cm D . 18 cm

答案解析收藏纠错 + 选题

二、填空题

11. (2021八上·青羊月考) 如图，长方体长、宽、高分别为4cm，3cm，12cm，则BD′=.

答案解析收藏纠错 + 选题
12. (2021八上·滕州月考) 印度数学家什迦罗（1141年-1225年）曾提出过“荷花问题”：平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边；渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？如图所示：荷花茎与湖面的交点为O ，点O距荷花的底端A的距离为0.5尺；被强风吹一边后，荷花底端与湖面交于点B ，点B到点O的距离为2尺，则湖水深度 $\text{[math]}$ 的长是尺．

答案解析收藏纠错 + 选题
13. (2021八上·滕州月考) 如图是一棵勾股树，它是由正方形和直角三角形排成的，若正方形A，B，C，D的边长分别是4，5，3，4，则最大正方形E的面积是．

答案解析收藏纠错 + 选题
14. (2021九上·沈阳开学考) 如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中（纸片在结合部分不重叠无缝隙），则图2中阴影部分面积为．

答案解析收藏纠错 + 选题
15. (2021九上·北京开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为边向外作正方形，面积分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. 如图所示，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点(不含端点B，C)，若线段AD的长为正整数，则点D的个数共有

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·吉林月考) 如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点．已知∠BAC=60°，∠DAE=45°，点D到地面的垂直距离DE=3 $\text{[math]}$ m，求点B到地面的垂直距离BC ．

答案解析收藏纠错 + 选题
18. 我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是多少尺？

答案解析收藏纠错 + 选题
19. (2021九上·黄石月考) △ABC中，∠B=90°，AB=5cm，BC=6cm，点P从点A开始沿边AB向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发，当点Q运动到点C时，两点停止运动.设运动时间为t秒.
1. （1）填空：BQ=，PB= （用含t的代数式表示）；
2. （2）当t为何值时，PQ的长度等于5cm？
3. （3）是否存在t的值，使得△PBQ的面积等于4cm²？若存在，请求出此时t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
20. (2022八上·雁塔期中) 已知等腰三角形ABC的底边BC＝2 $\text{[math]}$ cm ， D是腰AB上一点，且CD＝4cm ， BD＝2cm ．
1. （1）求证：CD⊥AB；
2. （2）求△ABC的面积．
答案解析收藏纠错 + 选题
21. 如图，BF是△ABC的角平分线，E为BC上一点，EF∥AB，过点E作BF的垂线，垂足为G，并交CA的延长线于点D，连结BD.
1. （1）求证：FG＝BG；
2. （2）当∠DBC＝90°，CF＝4，EB＝3时，求DE的长.
答案解析收藏纠错 + 选题
22. (2021·永州) 已知锐角△ABC中，角A、B、C的对边分别为a、b、c，边角总满足关系式： $\text{[math]}$ ＝ $\text{[math]}$ ＝ $\text{[math]}$ .
1. （1）如图1，若a＝6，∠B＝45°，∠C＝75°，求b的值；
2. （2）某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD（如图2所示），若CD⊥AB，AC＝14米，AB＝10米，sin∠ACB＝ $\text{[math]}$ ，求景观桥CD的长度.
答案解析收藏纠错 + 选题
23. (2021九上·香坊开学考) 在四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，过点A作AE⊥BC于点E．
1. （1）如图1，求证：AE＝CE；
2. （2）如图2，点F是线段CE．上一点，CF＝BE，FG⊥BC交BD于点G，连接AG，求证：AG＝BE+FG；
3. （3）如图3，在（2）的条件下，若EF＝10，FG＝7，求AG的长．
答案解析收藏纠错 + 选题
24. (2021九下·广西模拟) （阅读理解）
截长补短法，是初中数学几何题中一种辅助线的添加方法，截长就是在长边上载取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题.
1. （1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系.
  
  解题思路：延长DC到点E，使CE＝BD.连接AE，根据∠BAC＋∠BDC＝180°，可证∠ABD＝∠ACE，易证得△ABD≌△ACE，得出△ADE是等边三角形，所以AD＝DE，从而探寻线段DA、DB、DC之间的数量关系.
  
  根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是
2. （2）（拓展延伸）
  如图2，在Rt△ABC中，∠BAC＝90°，AB＝AC.若点D是边BC下方一点，∠BDC＝90°，探索线段DA、DB、DC之间的数量关系，并说明理由；
3. （3）（知识应用）
  如图3，一副三角尺斜边长都为14cm，把斜边重叠摆放在一起，则两块三角尺的直角顶点之间的距离PQ的长为cm.
答案解析收藏纠错 + 选题